Question

在二项式(ax^m+bxⁿ)¹²(a＞0,b＞0,m、n≠0)中有2m+n=0，如果它的展开式里最大系数项恰是常数项.

(1)求它是第几项?

(2)求的范围.

Answer 1

解:（1）设T_r+1=C^r₁₂(ax^m)^12-r·(bxⁿ)^r=C^r₁₂a^12-rb^rx^m(12-r)+nr为常数项，则有m(12-r)+nr=0，即m(12-r)-2mr=0,

    ∴r=4,它是第5项.

    （2）∵第5项又是系数最大的项，

    ∴有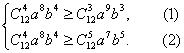

    由①得a⁸b⁴≥a⁹b³.

    ∵a＞0,b＞0,

    ∴b≥a,即≤.

    由②得≥,

    ∴≤≤.