题目内容
已知函数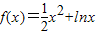
(1)若x=e为y=f(x)-2ex-ax的极值点,求实数a的值
(2)若x是函数f(x)的一个零点,且x∈(b,b+1),其中b∈N,则求b的值
(3)若当x≥1时
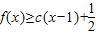 ,求c的取值范围.
,求c的取值范围.
【答案】分析:(1)由已知函数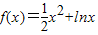 ,y=f(x)-2ex-ax,我们易求出函数y=f(x)-2ex-ax的解析式,又由进而求出其导函数的解析式,又由x=e为y=f(x)-2ex-ax的极值点,故y'x=e=0,由此构造关于a的方程,解方程即可求出实数a的值
,y=f(x)-2ex-ax,我们易求出函数y=f(x)-2ex-ax的解析式,又由进而求出其导函数的解析式,又由x=e为y=f(x)-2ex-ax的极值点,故y'x=e=0,由此构造关于a的方程,解方程即可求出实数a的值
(2)根据函数单调性的性质,我们易得函数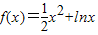 为增函数,若x是函数f(x)的一个零点,利用二分法我们易得在区间(
为增函数,若x是函数f(x)的一个零点,利用二分法我们易得在区间( ,1)上存在函数唯一的零点,则(
,1)上存在函数唯一的零点,则(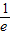 ,1)?(b,b+1),又由b∈N,即求出b的值
,1)?(b,b+1),又由b∈N,即求出b的值
(3)构造函数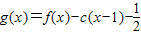 ,则问题可转化为当x≥1时函数恒成立问题,分析函数的单调性,求出函数的最值,即可求出c的取值范围.
,则问题可转化为当x≥1时函数恒成立问题,分析函数的单调性,求出函数的最值,即可求出c的取值范围.
解答:解:(1)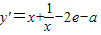 …(2分)
…(2分)
∵y在x=e处取得极值,∴y'x=e=0即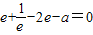 解得
解得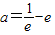
经检验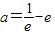 符合题意,∴
符合题意,∴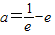 …(4分)
…(4分)
(2)∵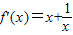 ,(x>0),∴f'(x)>0
,(x>0),∴f'(x)>0
∴f(x)在(0,+∞)上单调递增…(5分)
又∴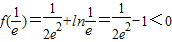
且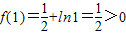
由二分法可得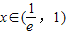 …(7分)
…(7分)
又∵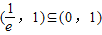
∴b=0…(8分)
(3)设 ,
,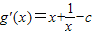 ,∵x≥1,∴
,∵x≥1,∴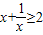
(ⅰ)若c≤2,当x≥1时,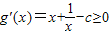 恒成立
恒成立
故g(x)在(0,+∞)上为增函数,
所以,x≥1时,g(x)≥g(1),即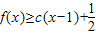 .…(9分)
.…(9分)
若c>2,方程g'(x)=0有2根
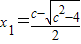 或
或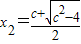 且x1<1<x2
且x1<1<x2
此时若x∈(1,x2),则g'(x)<0,
故g(x)在该区间为减函数
所以x∈(1,x2)时,g(x)<g(1)=0即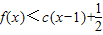
与题设 矛盾
矛盾
综上,满足条件的c的取值范围是(-∞,2]…(12分)
点评:本题考查的知识点是函数在某点取得极值的条件,函数恒成立问题,函数的零点,其中(1)的关键是根据函数在某点取得极值的条件构造方程y'x=e=0,(2)的关键是用二分法求出在区间(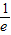 ,1)上存在函数唯一的零点,(3)的关键是将问题转化为一个函数恒成立问题.
,1)上存在函数唯一的零点,(3)的关键是将问题转化为一个函数恒成立问题.
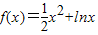 ,y=f(x)-2ex-ax,我们易求出函数y=f(x)-2ex-ax的解析式,又由进而求出其导函数的解析式,又由x=e为y=f(x)-2ex-ax的极值点,故y'x=e=0,由此构造关于a的方程,解方程即可求出实数a的值
,y=f(x)-2ex-ax,我们易求出函数y=f(x)-2ex-ax的解析式,又由进而求出其导函数的解析式,又由x=e为y=f(x)-2ex-ax的极值点,故y'x=e=0,由此构造关于a的方程,解方程即可求出实数a的值(2)根据函数单调性的性质,我们易得函数
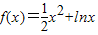 为增函数,若x是函数f(x)的一个零点,利用二分法我们易得在区间(
为增函数,若x是函数f(x)的一个零点,利用二分法我们易得在区间( ,1)上存在函数唯一的零点,则(
,1)上存在函数唯一的零点,则( ,1)?(b,b+1),又由b∈N,即求出b的值
,1)?(b,b+1),又由b∈N,即求出b的值(3)构造函数
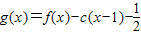 ,则问题可转化为当x≥1时函数恒成立问题,分析函数的单调性,求出函数的最值,即可求出c的取值范围.
,则问题可转化为当x≥1时函数恒成立问题,分析函数的单调性,求出函数的最值,即可求出c的取值范围.解答:解:(1)
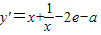 …(2分)
…(2分)∵y在x=e处取得极值,∴y'x=e=0即
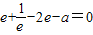 解得
解得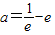
经检验
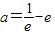 符合题意,∴
符合题意,∴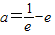 …(4分)
…(4分)(2)∵
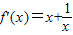 ,(x>0),∴f'(x)>0
,(x>0),∴f'(x)>0∴f(x)在(0,+∞)上单调递增…(5分)
又∴
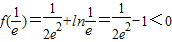
且
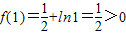
由二分法可得
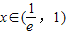 …(7分)
…(7分)又∵
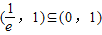
∴b=0…(8分)
(3)设
 ,
,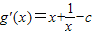 ,∵x≥1,∴
,∵x≥1,∴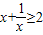
(ⅰ)若c≤2,当x≥1时,
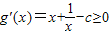 恒成立
恒成立故g(x)在(0,+∞)上为增函数,
所以,x≥1时,g(x)≥g(1),即
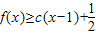 .…(9分)
.…(9分)若c>2,方程g'(x)=0有2根
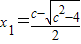 或
或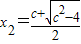 且x1<1<x2
且x1<1<x2此时若x∈(1,x2),则g'(x)<0,
故g(x)在该区间为减函数
所以x∈(1,x2)时,g(x)<g(1)=0即
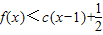
与题设
 矛盾
矛盾综上,满足条件的c的取值范围是(-∞,2]…(12分)
点评:本题考查的知识点是函数在某点取得极值的条件,函数恒成立问题,函数的零点,其中(1)的关键是根据函数在某点取得极值的条件构造方程y'x=e=0,(2)的关键是用二分法求出在区间(
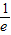 ,1)上存在函数唯一的零点,(3)的关键是将问题转化为一个函数恒成立问题.
,1)上存在函数唯一的零点,(3)的关键是将问题转化为一个函数恒成立问题. 
练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
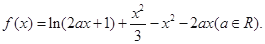
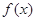 的极值点,求实数a的值;
的极值点,求实数a的值;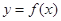 在
在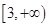 上为增函数,求实数a的取值范围.
上为增函数,求实数a的取值范围.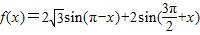
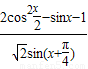 的值.
的值.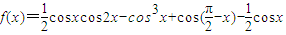
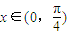 ,且
,且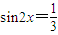 ,求f(x)的值.
,求f(x)的值.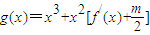 在区间(t,3)上有最值,求实数m取值范围;
在区间(t,3)上有最值,求实数m取值范围;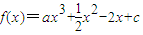
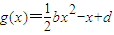 ,在(1)的条件下,是否存在实数b,使得函数g(x)的图象与函数f(x)的图象恒有含x=-1的三个不同交点?若存在,求出实数b的取值范围;否则说明理由.
,在(1)的条件下,是否存在实数b,使得函数g(x)的图象与函数f(x)的图象恒有含x=-1的三个不同交点?若存在,求出实数b的取值范围;否则说明理由.