题目内容
(文科)数列{an}是首项为21,公差d≠0的等差数列,记前n项和为Sn,若
S10和
S19的等比中项为
S16.数列{bn}满足:bn=anan+1an+2.
求:(1)数列{an}的通项an;(2)数列{bn}前n项和Tn最大时n的值.
| 1 |
| 10 |
| 1 |
| 19 |
| 1 |
| 16 |
求:(1)数列{an}的通项an;(2)数列{bn}前n项和Tn最大时n的值.
分析:(1)由首项为21,公差为d设出此等差数列的通项公式,以及前n项和公式,进而表示出
S10,
S19以及
S16,由
S10和
S19的等比中项为
S16,根据等比数列的性质列出关于d的方程,求出方程的解得到d的值,代入设出的通项公式即可得到数列{an}的通项an;
(2)令(1)求出的通项公式大于0,求出n的范围,进而得到n小于10,bn=anan+1an+2大于0,n大于11,bn=anan+1an+2小于0,根据递推公式Tn=Tn-1+bn,可得当bn>0时,Tn>Tn-1;当bn<0时,Tn<Tn-1,从而得到n小于10,,Tn}递增;当n大于11时,{Tn}递减,同时利用通项an,求出b10以及b11的值,即可得到数列{bn}前n项和Tn最大时n的值.
| 1 |
| 10 |
| 1 |
| 19 |
| 1 |
| 16 |
| 1 |
| 10 |
| 1 |
| 19 |
| 1 |
| 16 |
(2)令(1)求出的通项公式大于0,求出n的范围,进而得到n小于10,bn=anan+1an+2大于0,n大于11,bn=anan+1an+2小于0,根据递推公式Tn=Tn-1+bn,可得当bn>0时,Tn>Tn-1;当bn<0时,Tn<Tn-1,从而得到n小于10,,Tn}递增;当n大于11时,{Tn}递减,同时利用通项an,求出b10以及b11的值,即可得到数列{bn}前n项和Tn最大时n的值.
解答:解:(1)设an=21+(n-1)d(d≠0),
则Sn=21n+
d,
∴
Sn=21+
d,
∴
S10=21+
d,
S19=21+9d,
S16=21+
d.
由题设可知:(
S16)2=(
S10)•(
S19),
即(21+
d)2=(21+
d)•( 21+9d),解得d=-2,
∴an=21-2(n-1)=23-2n;
(2)由an=23-2n>0,得n<12.
∴当n<10时,bn=anan+1an+2>0;
当n>11时,bn=anan+1an+2<0.
而Tn=Tn-1+bn,
∴当bn>0时,Tn>Tn-1;当bn<0时,Tn<Tn-1.
∴当n<10时,{Tn}递增;当n>11时,{Tn}递减.
又b10=a10a11a12=-3,b11=a11a12a13=3,
∴T9=T11,
∴当n=9或11时,{ Tn}取最大值.
则Sn=21n+
| n(n-1) |
| 2 |
∴
| 1 |
| n |
| n-1 |
| 2 |
∴
| 1 |
| 10 |
| 9 |
| 2 |
| 1 |
| 19 |
| 1 |
| 16 |
| 15 |
| 2 |
由题设可知:(
| 1 |
| 16 |
| 1 |
| 10 |
| 1 |
| 19 |
即(21+
| 15 |
| 2 |
| 9 |
| 2 |
∴an=21-2(n-1)=23-2n;
(2)由an=23-2n>0,得n<12.
∴当n<10时,bn=anan+1an+2>0;
当n>11时,bn=anan+1an+2<0.
而Tn=Tn-1+bn,
∴当bn>0时,Tn>Tn-1;当bn<0时,Tn<Tn-1.
∴当n<10时,{Tn}递增;当n>11时,{Tn}递减.
又b10=a10a11a12=-3,b11=a11a12a13=3,
∴T9=T11,
∴当n=9或11时,{ Tn}取最大值.
点评:此题考查了等差数列的通项公式,求和公式,等比数列的性质,数列的递推式,以及数列的函数特征,熟练掌握公式及性质是解本题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
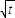 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.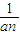 ),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值.
),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值.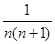 (n∈N*),若前n项的和为
(n∈N*),若前n项的和为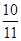 ,则项数为
,则项数为 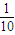 S10和
S10和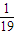 S19的等比中项为
S19的等比中项为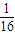 S16.数列{bn}满足:bn=anan+1an+2.
S16.数列{bn}满足:bn=anan+1an+2.