题目内容
给定一组函数解析式:①y=x| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
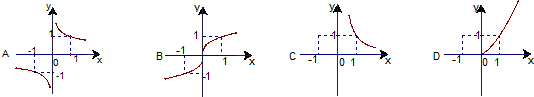
分析:分别根据幂函数的图象和性质进行判断即可.
解答:解::①y=x
定义域为[0,+∞),在定义域上单调递增,此时对应选项D.
②y=x-
定义域为(0,+∞),在定义域上单调递减,此时对应选项C.
③y=x
定义域为R,在定义域上单调递增,为奇函数,此时对应选项B.
④y=x-
定义域为{x|x≠0},在(0,+∞)上单调递减,此时对应选项A.
故答案为:④,③,②,①
| 3 |
| 2 |
②y=x-
| 3 |
| 2 |
③y=x
| 1 |
| 3 |
④y=x-
| 1 |
| 3 |
故答案为:④,③,②,①
点评:本题主要考查幂函数的图象和性质,根据幂函数的性质是解决本题的关键,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ;②
;② ;③
;③ ;④
;④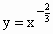 ;⑤
;⑤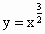 ;⑥
;⑥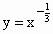 ;⑦
;⑦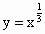 如图一组函数图象.请把图象对应的解析式号码填在图象下面的括号内.
如图一组函数图象.请把图象对应的解析式号码填在图象下面的括号内.
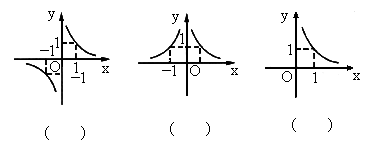
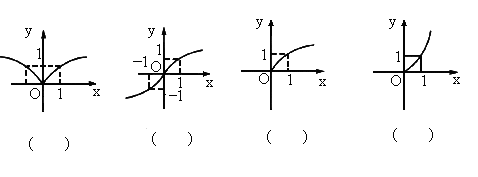
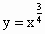 ;②
;②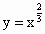 ;③
;③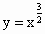 ;④
;④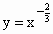 ;⑤
;⑤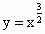 ;⑥
;⑥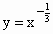 ;⑦
;⑦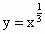 如图一组函数图象.请把图象对应的解析式号码填在图象下面的括号内.
如图一组函数图象.请把图象对应的解析式号码填在图象下面的括号内.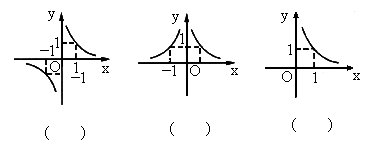

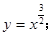 ②
② ③
③ ④
④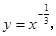 如图所示为一组函数图象,请把图象对应的解析式的号码填在相应图象下面的横线上.
如图所示为一组函数图象,请把图象对应的解析式的号码填在相应图象下面的横线上.