题目内容
当x>2时,使不等式x+ ≥a恒成立的实数a的取值范围是 .
≥a恒成立的实数a的取值范围是 .
【答案】分析:根据x>2,得到x-2>0,利用基本不等式可得(x-2)+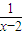
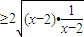 =2,再结合原不等式恒成立,可得到左边的最小值4大于或等于a,由此可得实数a的取值范围是a≤4.
=2,再结合原不等式恒成立,可得到左边的最小值4大于或等于a,由此可得实数a的取值范围是a≤4.
解答:解:∵x>2
∴x-2>0
∴x+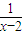 =(x-2)+
=(x-2)+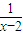 +2
+2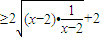 =4
=4
而不等式x+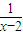 ≥a恒成立
≥a恒成立
∴(x+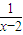 )min≥a
)min≥a
∴a的取值范围是(-∞,4]
故答案为(-∞,4]
点评:本题以分式不等式为例,考查了函数恒成立的知识,属于中档题.注意解法中配凑,然后用基本不等式的技巧,这是此类问题的常见处理方法.
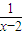
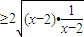 =2,再结合原不等式恒成立,可得到左边的最小值4大于或等于a,由此可得实数a的取值范围是a≤4.
=2,再结合原不等式恒成立,可得到左边的最小值4大于或等于a,由此可得实数a的取值范围是a≤4.解答:解:∵x>2
∴x-2>0
∴x+
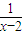 =(x-2)+
=(x-2)+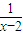 +2
+2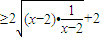 =4
=4而不等式x+
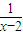 ≥a恒成立
≥a恒成立∴(x+
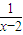 )min≥a
)min≥a∴a的取值范围是(-∞,4]
故答案为(-∞,4]
点评:本题以分式不等式为例,考查了函数恒成立的知识,属于中档题.注意解法中配凑,然后用基本不等式的技巧,这是此类问题的常见处理方法.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
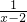 ≥a恒成立的实数a的取值范围是________.
≥a恒成立的实数a的取值范围是________.