题目内容
若不等式x2+2x+a≥-y2-2y对实数x,y都成立,则实数a范围是
| A. a≥0 | B. a≥1 | C. a≥2 | D.a≥3 |
C
解析试题分析:由题意可知,不等式x2+2x+a≥-y2-2y对实数x,y都成立,那么可知a≥-y2-2y-x2-2x
而对于-y2-2y-x2-2x=-(y+1)2-(x+1) 2+2 2,因此可知,a的取值范围就是右边表达式的最大值即可,即为a≥2,选C.
2,因此可知,a的取值范围就是右边表达式的最大值即可,即为a≥2,选C.
考点:本试题考查了不等式的运用。
点评:解决不等式的恒成立问题,主要是利用分离参数的思想,结合不等式的性质和函数的性质等来分析其取值范围即可,属于中档题。

练习册系列答案
相关题目
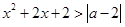 对于一切实数
对于一切实数 均成立,则实数
均成立,则实数 的取值范围是______.
的取值范围是______.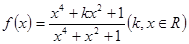 .则
.则 的最大值与最小值的乘积为 .
的最大值与最小值的乘积为 .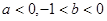 则下列不等式成立的是
则下列不等式成立的是 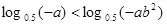
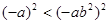
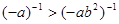
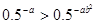
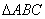 的内角
的内角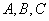 所对的边为
所对的边为 ;则下列命题正确的__________________
;则下列命题正确的__________________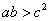 ;则
;则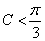
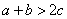 ;则
;则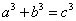 ;则
;则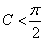
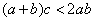 ;则
;则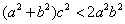 ;则
;则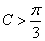
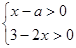 的整数解6个,则a的取值范围是____________.
的整数解6个,则a的取值范围是____________.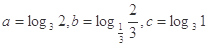 ,则
,则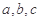 大小关系是_____________.
大小关系是_____________.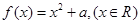 .
. ,比较
,比较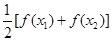 与
与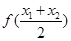 的大小;
的大小;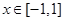 时,有
时,有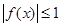 ,求实数
,求实数 的取值范围.
的取值范围.
