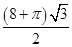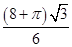题目内容
一平面截一球得到直径为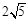 cm的圆面,球心到这个平面的距离是2 cm,则该球的体积是( )
cm的圆面,球心到这个平面的距离是2 cm,则该球的体积是( )
| A.12 cm3 | B.36cm3 | C.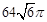 cm3 cm3 | D. cm3 cm3 |
B
解析试题分析:因为球心和截面圆心的连线垂直于截面,由勾股定理得,球半径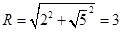 ,故球的体积为
,故球的体积为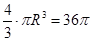
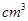 .
.
考点:1、球的截面性质;2、球的体积.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
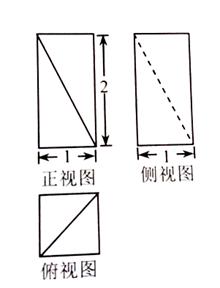
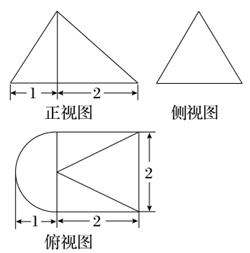
一个几何体的三视图如图所示,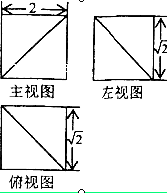
则该几何体的体积是( ).
A.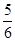 | B.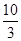 | C.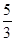 | D.2 |
正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数共有( )
| A.20 | B.15 | C.12 | D.10 |
[2013·江西高考]一几何体的三视图如图所示,则该几何体的体积为( )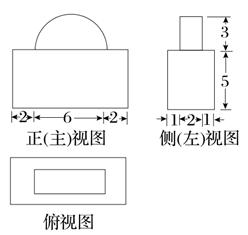
| A.200+9π | B.200+18π | C.140+9π | D.140+18π |
棱长为2的三棱锥的外接球的表面积为( )
| A.6π | B.4π | C.2π | D.π |
三棱锥 及其三视图中的正(主)视图和侧(左)视图如图所示,则棱SB的长为( )
及其三视图中的正(主)视图和侧(左)视图如图所示,则棱SB的长为( )
A.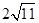 | B. | C. | D.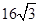 |
若两个球的表面积之比为1:4,则这两个球的体积之比为( )
| A.1:2 | B.1:4 | C.1:8 | D.1:16 |