题目内容
已知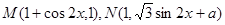
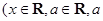 是常数),且
是常数),且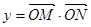 (其中
(其中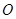 为坐标原点).
为坐标原点).
(1)求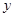 关于
关于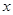 的函数关系式
的函数关系式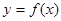 ;
;
(2)求函数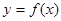 的单调区间;
的单调区间;
(3)若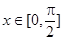 时,
时,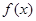 的最大值为4,求
的最大值为4,求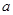 的值.
的值.
【答案】
(1) .(2)增区间为
.(2)增区间为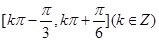 ,
,
单调递减区间为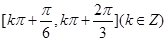 .(3)
.(3)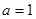 .
.
【解析】(1)数量积的坐标运算;(2)利用辅助角公式化简函数,由复合函数的单调性,解不等式;
(3)先确定得到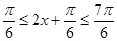 ,将
,将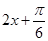 看作t,研究函数y=sint在
看作t,研究函数y=sint在 的最值情况。
的最值情况。
解:(1)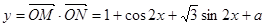 ,
,
所以 .
.
(2)由(1)可得 ,
,
由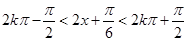 , 解得
, 解得 ;
;
由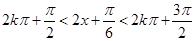 ,
解得
,
解得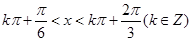 ,
,
所以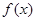 的单调递增区间为
的单调递增区间为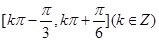 ,
,
单调递减区间为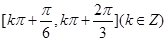 .
.
(3) ,因为
,因为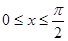 , 所以
, 所以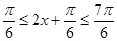 ,
,
当 ,即
,即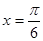 时,
时,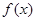 取最大值
取最大值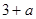 ,
,
所以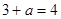 ,即
,即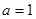 .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
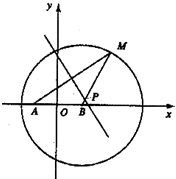 (2003•崇文区一模)已知圆B方程(x-c)2+y2=4a2(a>c>0,a,c是常数),且A(-c,0),点M在圆B上运动,线段AM的垂直平分线交MB于点P.
(2003•崇文区一模)已知圆B方程(x-c)2+y2=4a2(a>c>0,a,c是常数),且A(-c,0),点M在圆B上运动,线段AM的垂直平分线交MB于点P.