题目内容
在古希腊,毕达哥拉斯学派把1,3,6,10,15,……这些数叫做三角形数,因为这些数目的石子可以排成一个正三角形(如下图)则第八个三角形数是 ( )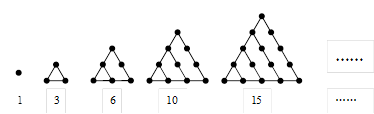
| A.35 | B.36 | C.37 | D.38 |
B
解析试题分析:根据题意,我们发现毕达哥拉斯学派把1,3,6,10,15,……这些数叫做三角形数,构成了这样一个规律,就是1+2=3,1+2+3=6,1+2+3+4=10,1+2+3+4+5=15,依次类推,第八个三角形中的数位1+2+3+4+5+6+7+8=36,故答案为B.
考点:数列的规律性
点评:主要是考查了数列的递推关系 运用,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设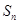 是等差数列
是等差数列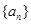 的前
的前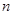 项和,若
项和,若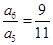 ,则
,则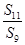 =( )
=( )
| A.1 | B.-1 | C.2 | D.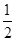 |
等差数列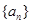 中,
中,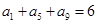 则
则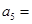 ( )
( )
| A.2 | B.3 | C.6 | D.±2 |
设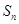 为等差数列
为等差数列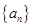 的前n项的和,
的前n项的和,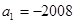 ,
,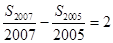 ,则
,则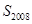 的值为( )
的值为( )
A.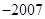 | B. | C.2007 | D.2008 |
在等差数列 中,
中,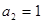 ,
,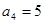 ,则
,则 的前5项和
的前5项和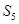 =
=
| A.7 | B.15 | C.20 | D.25 |
已知数列{an}的通项公式为an=4n-3,则a5的值是( )
| A.9 | B.13 | C.17 | D.21 |
公差不为零的等差数列 的前
的前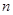 项和为
项和为 .若
.若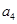 是
是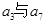 的等比中项,
的等比中项, 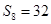 ,则
,则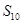 等于()
等于()
| A. 18 | B. 24 | C. 60 | D. 90 |
已知数列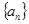 满足
满足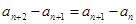 ,
,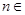 N*,且
N*,且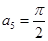 。若函数
。若函数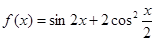 ,记
,记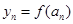 ,则
,则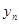 的前9项和为
的前9项和为
A. | B.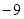 | C.9 | D.1 |
在等差数列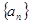 中,若
中,若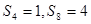 ,则
,则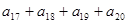 的值为( )
的值为( )
| A.9 | B.12 | C.16 | D.17 |