题目内容
球的表面积与它的内接正方体的表面积之比是( )
A． | B． | C． | D． |
B
解析试题分析：因为球的直径2R就是球的内接正方体的体对角线的长
.即
.所以球的表面积为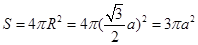
.因为内接正方体的表面积为
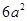.所以球的表面积与它的内接正方体的表面积之比是.故选B.
考点：1.球的与内接正方体的关系.2.球的表面积公式.3.正方体的表面积公式.
练习册系列答案
备战中考寒假系列答案
相关题目
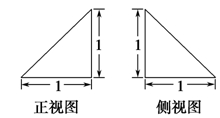
一空间几何体的三视图如右图所示,则该几何体的体积为（ ）
A． | B． | C． | D． |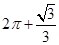
某几何体的三视图如右图所示，则它的表面积是（ ）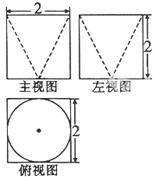
A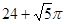． | B． | C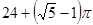． | D． |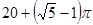
已知某几何体的三视图（单位:
）如图所示，则此几何体的体积是( )
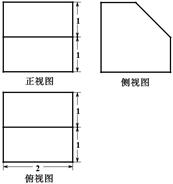
A．1 | B．3 | C．5 | D．7 |
三条侧棱两两互相垂直且长都为
的三棱锥的四个顶点全部在同一个球面上，则该球的表面积为（ ）
A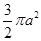． | B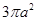． | C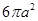． | D． |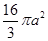
某几何体三视图及相关数据如右图所示，则该几何体的体积为 （ ）
| A．16 | B．16 | C．64+16 | D．16+ |
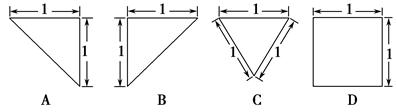
一个几何体的三视图如下图所示，这个几何体可能是一个（ ）
| A．三棱锥 | B．底面不规则的四棱锥 |
| C．三棱柱 | D．底面为正方形的四棱锥 |
已知某几何体的三视图如下图所示，则该几何体的表面积是( )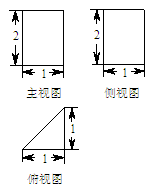
A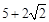． | B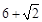． | C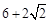． | D． |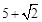
