题目内容
若π≤x≤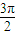
，则方程2sinx+1=0的解x= ．
【答案】分析：根据2sinx+1=0，得sinx=-
．结合sin
=
和诱导公式sin（π+α）=-sinα，可得x的值．
解答：解：∵2sinx+1=0，∴sinx=-
∵π≤x≤
，
∴x=π+
=
故答案为：
点评：本题给出角的范围和角的正弦值，求角的大小，着重考查了诱导公式和特殊角的三角函数值等知识，属于基础题．
．结合sin=和诱导公式sin（π+α）=-sinα，可得x的值．解答：解：∵2sinx+1=0，∴sinx=-
∵π≤x≤
，∴x=π+
=故答案为：
点评：本题给出角的范围和角的正弦值，求角的大小，着重考查了诱导公式和特殊角的三角函数值等知识，属于基础题．
练习册系列答案
相关题目