题目内容
若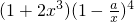 的展开式中的常数项是65,则a的值为
的展开式中的常数项是65,则a的值为
- A.-2
- B.-1
- C.1
- D.2
A
分析:将已知的式子按多项式展开,将已知式子展开式的常数项问题转化为二项式的系数问题;利用二项展开式的通项公式求出二项式展开式的通项,求出其常数项与x-3的系数;列出方程求出a的值.
解答:∵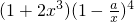 =
=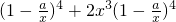
∴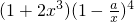 的展开式中的常数项是=
的展开式中的常数项是=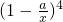 的常数项与
的常数项与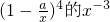 的系数的2倍.
的系数的2倍.
∵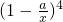 展开式的通项为Tr+1=(-a)rC4rx-r
展开式的通项为Tr+1=(-a)rC4rx-r
当r=0时,得到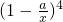 的常数项为1,
的常数项为1,
当r=3时,得到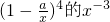 的系数为(-a)3C43=-4a3
的系数为(-a)3C43=-4a3
所以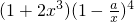 展开式的常数项为1-8a3=65
展开式的常数项为1-8a3=65
解得a=-2.
故选A.
点评:本题考查等价转化的能力、考查求二项展开式的特定项问题时,常利用二项展开式的通项公式.
分析:将已知的式子按多项式展开,将已知式子展开式的常数项问题转化为二项式的系数问题;利用二项展开式的通项公式求出二项式展开式的通项,求出其常数项与x-3的系数;列出方程求出a的值.
解答:∵
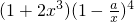 =
=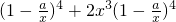
∴
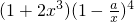 的展开式中的常数项是=
的展开式中的常数项是=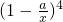 的常数项与
的常数项与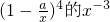 的系数的2倍.
的系数的2倍.∵
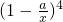 展开式的通项为Tr+1=(-a)rC4rx-r
展开式的通项为Tr+1=(-a)rC4rx-r当r=0时,得到
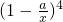 的常数项为1,
的常数项为1,当r=3时,得到
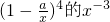 的系数为(-a)3C43=-4a3
的系数为(-a)3C43=-4a3所以
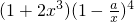 展开式的常数项为1-8a3=65
展开式的常数项为1-8a3=65解得a=-2.
故选A.
点评:本题考查等价转化的能力、考查求二项展开式的特定项问题时,常利用二项展开式的通项公式.

练习册系列答案
相关题目
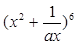 的展开式中的常数项为
的展开式中的常数项为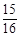 ,则实数
,则实数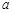 等于
等于 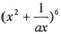 的展开式中的常数项为
的展开式中的常数项为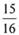 ,则实数a = ______.
,则实数a = ______.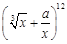 的展开式中的常数项为
的展开式中的常数项为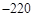 ,则实数
,则实数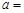 ___________.
___________.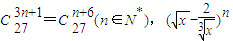 的展开式中的常数项是 (用数字作答).
的展开式中的常数项是 (用数字作答).