题目内容
已知下表中的对数值有且只有两个是错误的.| x | 1.5 | 3 | 5 | 6 | 7 | 8 | 9 | 14 | 27 |
| lgx | 3a-b+c | 2a-b | a+c | 1+a-b-c | 2(a+c) | 3(1-a-c) | 2(2a-b) | 1-a+2b | 3(2a-b) |
(2)求证lg3的对数值是正确的;
(3)试将两个错误的对数值均指出来,并加以改正(不要求证明)
【答案】分析:(1)由lg5=a+c,可推知lg2=1-a-c,lg6=lg2+lg3=1+a-b-c再判断.
(2)用反证法,先假设lg3=2a-b是错误的,根据题意转化为lg3≠2a-b,lg9=2lg3≠2(2a-b),lg27=3lg3≠3(2a-b),进而得知lg9,lg27也均是错误的得证.
(3)由(2)知lg3一定对,可知lg9,lg27都对.若lg5错,则lg6,lg8均错,得知lg5对,转化为lg2=1-a-c,推知lg6,lg8均对的.
解答:解:(1)由lg5=a+c,得lg2=1-a-c∴lg6=lg2+lg3=1+a-b-c满足表中数值,也就是lg6在假设下是正确的.(4分)
(2)假设lg3=2a-b是错误的,即lg3≠2a-b,∴lg9=2lg3≠2(2a-b),lg27=3lg3≠3(2a-b)
于是lg9,lg27也均是错误的,
这与“有且只有两个是错误的”矛盾,故假设不成立,
∴lg3的对数值是正确的.(8分)
(3)lg1.5是错误的,正确值应为3a-b+c-1(12分)lg7是错误的,正确值应为2b+c(16分)
理由:由(2)知lg3一定对,则lg9,lg27都对.若lg5错,则lg6,lg8均错(不符),
所以lg5对的,可得lg2=1-a-c,即有lg6,lg8均对的.
∴lg1.5=lg3-lg2=3a-b+c-1,
∴表中lg1.5是错的.又易知lg7是错的,
∵2(a+c)=2lg5=lg25≠lg7,事实上lg7=lg14-lg2=2b+c
点评:本题主要考查数的关系和反证法的应用,要注意基本步骤,先否定结论,肯定假设,推出矛盾,肯定结论,否定假设.
(2)用反证法,先假设lg3=2a-b是错误的,根据题意转化为lg3≠2a-b,lg9=2lg3≠2(2a-b),lg27=3lg3≠3(2a-b),进而得知lg9,lg27也均是错误的得证.
(3)由(2)知lg3一定对,可知lg9,lg27都对.若lg5错,则lg6,lg8均错,得知lg5对,转化为lg2=1-a-c,推知lg6,lg8均对的.
解答:解:(1)由lg5=a+c,得lg2=1-a-c∴lg6=lg2+lg3=1+a-b-c满足表中数值,也就是lg6在假设下是正确的.(4分)
(2)假设lg3=2a-b是错误的,即lg3≠2a-b,∴lg9=2lg3≠2(2a-b),lg27=3lg3≠3(2a-b)
于是lg9,lg27也均是错误的,
这与“有且只有两个是错误的”矛盾,故假设不成立,
∴lg3的对数值是正确的.(8分)
(3)lg1.5是错误的,正确值应为3a-b+c-1(12分)lg7是错误的,正确值应为2b+c(16分)
理由:由(2)知lg3一定对,则lg9,lg27都对.若lg5错,则lg6,lg8均错(不符),
所以lg5对的,可得lg2=1-a-c,即有lg6,lg8均对的.
∴lg1.5=lg3-lg2=3a-b+c-1,
∴表中lg1.5是错的.又易知lg7是错的,
∵2(a+c)=2lg5=lg25≠lg7,事实上lg7=lg14-lg2=2b+c
点评:本题主要考查数的关系和反证法的应用,要注意基本步骤,先否定结论,肯定假设,推出矛盾,肯定结论,否定假设.

练习册系列答案
相关题目
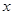
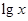
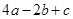
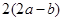
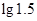 B.
B.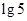 C.
C.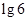 D.
D.

 B.
B. C.
C. D.
D.