题目内容
已知一个半径为R的球有一个内接正方体（即正方体的顶点都在球面上），求这个球的球面面积与其内接正方体的全面积之比．
分析：设球的半径为R，则正方体的对角线长为2R，求出正方体的表面积和球的表面积，从而得出球的球面面积与其内接正方体的全面积之比．
解答：解：设球的半径为R，内接正方体的棱长为a．
则正方体的对角线长为2R，
依题意知 2R=
a，则
=
∴S球=4πR2，S正方体=6a2，
这个球的球面面积与其内接正方体的全面积之比=
=
•(
)2=
•
=
．
则正方体的对角线长为2R，
依题意知 2R=
| 3 |
| R |
| a |
| ||
| 2 |
∴S球=4πR2，S正方体=6a2，
这个球的球面面积与其内接正方体的全面积之比=
| 4πR2 |
| 6a2 |
| 2π |
| 3 |
| R |
| a |
| 2π |
| 3 |
| 3 |
| 4 |
| π |
| 2 |
点评：本题是基础题，解题的突破口是正方体的体对角线就是球的直径，正确进行正方体的表面积的计算，是解好本题的关键，考查计算能力．
练习册系列答案
相关题目
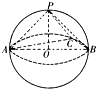如图所示，已知三棱锥P-ABC的各顶点均在一个半径为R的球面上，球心0在AB上，P0⊥平面ABC，