题目内容
已知P(x,y)是直线 上一动点,PA,PB是圆C:
上一动点,PA,PB是圆C: 的两条切线,A、B是切点,若四边形PACB的最小面积是2,则
的两条切线,A、B是切点,若四边形PACB的最小面积是2,则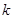 的值为
的值为
A.3 B. C.
C. D.2
D.2
D
解析试题分析:根据题意,由于P(x,y)是直线 上一动点,PA,PB是圆C:
上一动点,PA,PB是圆C: 的两条切线,A、B是切点,那么可由切线长定理,以及四边形PACB的最小面积即为圆心到点P的距离的最小时得到,那么根据点到直线的距离公式可知,d=
的两条切线,A、B是切点,那么可由切线长定理,以及四边形PACB的最小面积即为圆心到点P的距离的最小时得到,那么根据点到直线的距离公式可知,d= =1.可知斜率k=1,故答案为D.
=1.可知斜率k=1,故答案为D.
考点:直线与圆的位置关系
点评:主要是考查了直线与圆的位置关系的运用,属于基础题。

练习册系列答案
相关题目
过点 作圆
作圆 的弦,其中弦长为整数的共有( )
的弦,其中弦长为整数的共有( )
| A.16条 | B.17条 | C.32条 | D.34条 |
圆 截直线
截直线 所得弦长是( )
所得弦长是( )
| A.2 | B.1 | C. | D. |
若直线 与圆
与圆 有公共点,则实数a取值范围是( )
有公共点,则实数a取值范围是( )
| A.[-3,-1] | B.[-1,3] |
| C.[-3,l ] | D.(-∞,-3]  [1.+∞) [1.+∞) |
在圆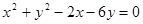 内,过点
内,过点 的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为
的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为
A.5 | B.10 | C.15 | D.20 |
已知 ,则以
,则以 为直径的圆的方程是( )
为直径的圆的方程是( )
A. | B. |
C. | D. |
直线 与圆
与圆 相交于
相交于 ,
, 两点,且
两点,且 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
下列满足“与直线 平行,且与圆
平行,且与圆 相切”的是( )
相切”的是( )
A.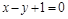 | B. |
C. | D. |
 中,圆
中,圆 的方程为
的方程为 ,若直线
,若直线 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆 的取值范围是( )
的取值范围是( )
 或
或
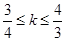
 或
或