题目内容
四个纪念币A、B、C、D,投掷时正面向上的概率如下表所示(0<a<1).| 纪念币 | A | B | C | D |
| 概率 |  |  | a | a |
(1)求ξ的分布列及数学期望;
(2)在概率P (ξ=i ) (i=0,1,2,3,4)中,若P (ξ=2 )的值最大,求a的取值范围.
【答案】分析:(1)其中ξ的可能取值为0,1,2,3,4,然后根据n次独立重复试验中恰好发生k次的概率公式求出相应的概率,列出分布列,最后利用数学期望公式解之即可;
(2)根据0<a<1可知P (ξ=0)<P (ξ=1),P (ξ=4)<P (ξ=3)只需P (ξ=2)-P (ξ=1)≥0且P (ξ=2)-P (ξ=3)≥0,解之即可求出a的取值范围.
解答:解:(1)P (ξ)是ξ个正面向上的概率,其中ξ的可能取值为0,1,2,3,4.
∴P (ξ=0)=C2(1- )2C2(1-a)2=
)2C2(1-a)2= (1-a)2,
(1-a)2,
P (ξ=1)=C21• (1-
(1- )C2(1-a)2+C2(1-
)C2(1-a)2+C2(1- )2C21a(1-a)=
)2C21a(1-a)= (1-a)
(1-a)
P (ξ=2)=C22•( )2C2(1-a)2+C21•
)2C2(1-a)2+C21• (1-
(1- )C21a(1-a)+C2(1-
)C21a(1-a)+C2(1- )2C22a2=
)2C22a2= (1+2a-2a2),
(1+2a-2a2),
P (ξ=3)=C22•( )2C21a(1-a)+C21•
)2C21a(1-a)+C21• (1-
(1- )C22a2=
)C22a2= ,
,
P (ξ=4)=C22( )2C22a2=
)2C22a2= a2.
a2.
∴ξ的分布列为:
∴ξ的数学期望为:Eξ=0× (1-a)2+1×
(1-a)2+1× (1-a)+2×
(1-a)+2× (1+2a-2a2)+3×
(1+2a-2a2)+3× +4×
+4× a2=2a+1.(7分)
a2=2a+1.(7分)
(2)∵0<a<1,∴P (ξ=0)<P (ξ=1),P (ξ=4)<P (ξ=3)
则P (ξ=2)-P (ξ=1)= (1+2a-2a2)-
(1+2a-2a2)- (1-a)=-
(1-a)=- (2a2-4a+1)≥0
(2a2-4a+1)≥0
P (ξ=2)-P (ξ=3)= (1+2a-2a2)-
(1+2a-2a2)- =-
=- (2a2-1)≥0
(2a2-1)≥0
由 ,得
,得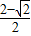 ≤a≤
≤a≤ ,
,
即a的取值范围是[ ,
,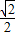 ].(12分)
].(12分)
点评:本题主要考查了n次独立重复试验中恰好发生k次的概率,以及离散型随机变量的概率分布与数学期望,同时考查了计算能力,属于中档题.
(2)根据0<a<1可知P (ξ=0)<P (ξ=1),P (ξ=4)<P (ξ=3)只需P (ξ=2)-P (ξ=1)≥0且P (ξ=2)-P (ξ=3)≥0,解之即可求出a的取值范围.
解答:解:(1)P (ξ)是ξ个正面向上的概率,其中ξ的可能取值为0,1,2,3,4.
∴P (ξ=0)=C2(1-
 )2C2(1-a)2=
)2C2(1-a)2= (1-a)2,
(1-a)2,P (ξ=1)=C21•
 (1-
(1- )C2(1-a)2+C2(1-
)C2(1-a)2+C2(1- )2C21a(1-a)=
)2C21a(1-a)= (1-a)
(1-a)P (ξ=2)=C22•(
 )2C2(1-a)2+C21•
)2C2(1-a)2+C21• (1-
(1- )C21a(1-a)+C2(1-
)C21a(1-a)+C2(1- )2C22a2=
)2C22a2= (1+2a-2a2),
(1+2a-2a2),P (ξ=3)=C22•(
 )2C21a(1-a)+C21•
)2C21a(1-a)+C21• (1-
(1- )C22a2=
)C22a2= ,
,P (ξ=4)=C22(
 )2C22a2=
)2C22a2= a2.
a2.∴ξ的分布列为:
| ξ | 1 | 2 | 3 | 4 | |
| P |  (1-a)2 (1-a)2 |  (1-a) (1-a) |  (1+2a-2a2) (1+2a-2a2) |  |  a2 a2 |
 (1-a)2+1×
(1-a)2+1× (1-a)+2×
(1-a)+2× (1+2a-2a2)+3×
(1+2a-2a2)+3× +4×
+4× a2=2a+1.(7分)
a2=2a+1.(7分)(2)∵0<a<1,∴P (ξ=0)<P (ξ=1),P (ξ=4)<P (ξ=3)
则P (ξ=2)-P (ξ=1)=
 (1+2a-2a2)-
(1+2a-2a2)- (1-a)=-
(1-a)=- (2a2-4a+1)≥0
(2a2-4a+1)≥0P (ξ=2)-P (ξ=3)=
 (1+2a-2a2)-
(1+2a-2a2)- =-
=- (2a2-1)≥0
(2a2-1)≥0由
 ,得
,得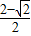 ≤a≤
≤a≤ ,
,即a的取值范围是[
 ,
,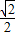 ].(12分)
].(12分)点评:本题主要考查了n次独立重复试验中恰好发生k次的概率,以及离散型随机变量的概率分布与数学期望,同时考查了计算能力,属于中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
(本题满分12分)
四个纪念币A、B、C、D,投掷时正面向上的概率如下表所示(0<a<1)
| 纪念币 | A | B | C | D |
| 概率 | 1/2 | 1/2 | a | a |
这四个纪念币同时投掷一次,设ξ表示出正面向上的个数。
(1)求概率p(ξ)
(2)求在概率p(ξ),p(ξ=2)为最大时,a的取值范围。
(3)求ξ的数学期望。

