题目内容
已知函数![]() (a∈R).
(a∈R).
(Ⅰ)当![]() 时,求
时,求![]() 的极值;
的极值;
(Ⅱ)当![]() 时,求
时,求![]() 单调区间;
单调区间;
(Ⅲ)若对任意![]() 及
及![]() ,恒有
,恒有![]()
成立,求实数m的取值范围.
(1)![]() 的极小值为
的极小值为![]() ,无极大值(2)见解析(3)m≤
,无极大值(2)见解析(3)m≤![]()
解析:
(Ⅰ)依题意知![]() 的定义域为
的定义域为![]()
当![]() 时,
时,![]() 令
令![]() ,解得
,解得![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
又∵![]() ∴
∴![]() 的极小值为
的极小值为![]() ,无极大值
,无极大值
(Ⅱ)![]()
当![]() 时,
时,![]() ,令
,令![]() ,得
,得![]() ,令
,令![]() 得
得![]()
当![]() 时,得
时,得![]() ,令
,令![]() 得
得![]() 或
或![]() ;
;
令![]() 得
得![]() ;当
;当![]() 时,
时,![]()
综上所述,当![]() 时,
时,![]() 的递减区间为
的递减区间为![]() 和
和![]() ,递增区间为
,递增区间为![]() ;
;
当![]() 时,
时,![]() 在
在![]() 单调递减;当
单调递减;当![]() 时,
时,![]() 的递减区间为
的递减区间为![]() 和
和![]() ,递增区间为
,递增区间为![]() .
.
(Ⅲ)由(Ⅱ)可知,当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减.
上单调递减.
当![]() 时,
时,![]() 取最大值;当
取最大值;当![]() 时,
时,![]() 取最小值;
取最小值;
![]()
![]()
![]()
∵![]() 恒成立,
恒成立,
∴![]()
整理得![]() ,∵
,∵![]() ,∴
,∴![]() 恒成立,∵
恒成立,∵![]() ,
,
∴![]() ,∴m≤
,∴m≤![]()

练习册系列答案
相关题目
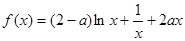 (a∈R).
(a∈R).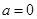 时,求
时,求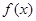 的极值;
的极值;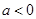 时,求
时,求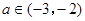 及
及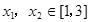 ,恒有
,恒有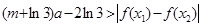
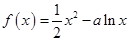 (a∈R)
(a∈R)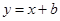 ,求a,b的值;
,求a,b的值;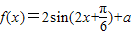 a∈R,a是常数
a∈R,a是常数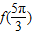 的值
的值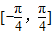 上的最大值与最小值之和为
上的最大值与最小值之和为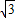 ,求实数a的值.
,求实数a的值.