题目内容
若扇形的圆心角是
，半径为R，则扇形的内切圆面积与扇形的面积之比为（ ）
| π |
| 3 |
分析：确定扇形的内切圆的半径，分别计算扇形的内切圆面积与扇形的面积，即可得到结论．
解答：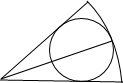
解：∵扇形的圆心角是
，半径为R，
∴S扇形=
lR=
∵扇形的内切圆的圆心在圆心角的角平分线上，
∴几何知识，r+2r=R，所以内切圆的半径为
，
∴S圆形=
，
∴扇形的内切圆面积与扇形的面积之比为
：
=
故选C．
解：∵扇形的圆心角是| π |
| 3 |
∴S扇形=
| 1 |
| 2 |
| πR2 |
| 6 |
∵扇形的内切圆的圆心在圆心角的角平分线上，
∴几何知识，r+2r=R，所以内切圆的半径为
| R |
| 3 |
∴S圆形=
| πR2 |
| 9 |
∴扇形的内切圆面积与扇形的面积之比为
| πR2 |
| 9 |
| πR2 |
| 6 |
| 2 |
| 3 |
故选C．
点评：本题考查扇形的面积公式，考查学生的计算能力，确定扇形的内切圆的半径是关键．
练习册系列答案
相关题目
，半径为R，则扇形的内切圆面积与扇形的面积之比为
，半径为R，则扇形的内切圆面积与扇形的面积之比为（ ）