题目内容
已知矩形ABCD的顶点都在半径为4的球O的球面上,且AB=6,BC=2| 3 |
分析:由题意求出矩形的对角线的长,结合球的半径,球心到矩形的距离,满足勾股定理,求出棱锥的高,即可求出棱锥的体积.
解答:解:矩形的对角线的长为:
=4
,所以球心到矩形的距离为:
=2,
所以棱锥O-ABCD的体积为:
×6×2
×2=8
.
故答案为:8
62+(2
|
| 3 |
42-(2
|
所以棱锥O-ABCD的体积为:
| 1 |
| 3 |
| 3 |
| 3 |
故答案为:8
| 3 |
点评:本题是基础题,考查球内几何体的体积的计算,考查计算能力,空间想象能力,常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
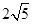 ,则棱锥O-ABCD的侧面积为( )
,则棱锥O-ABCD的侧面积为( )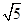 B. 44 C、20
B. 44 C、20