题目内容
求函数定义域(要求列出不等式然后写出答案,解不等式过程不写)
(1)y=logsinx(cosx+
);
(2)y=
+ln(4-x2).
(1)y=logsinx(cosx+
| 1 |
| 2 |
(2)y=
| tanx-1 |
分析:(1)要保证底数大于0且不等于1,真数大于0,由此列出不等式组,解出即可;
(2)保证被开方数大于等于0,且真数大于0,列出不等式组,解出即可.
(2)保证被开方数大于等于0,且真数大于0,列出不等式组,解出即可.
解答:解:(1)由
,解得2kπ<x<
π+2kπ,且x≠
+2kπ,k∈Z.
所以函数的定义域为:{x|2kπ<x<
π+2kπ,且x≠
+2kπ,k∈Z}.
(2)由
,即
.解得-2<x<-
,或
≤x<
.
所以函数的定义域为:{x|-2<x<-
,或
≤x<
}.
|
| 2 |
| 3 |
| π |
| 2 |
所以函数的定义域为:{x|2kπ<x<
| 2 |
| 3 |
| π |
| 2 |
(2)由
|
|
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
所以函数的定义域为:{x|-2<x<-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
点评:本题考查函数定义域的求解,解析法给出的函数,要保证各部分均有意义.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 .
. 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 ;
; 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数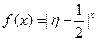 在定义域内单调递增”为事件
在定义域内单调递增”为事件 ,求事件
,求事件 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 。
。 为攻关期满时获奖小组的个数,求
为攻关期满时获奖小组的个数,求 为攻关期满时获奖小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖小组数与没有获奖的攻关小组数之差的平方,记“函数 在定义域内单调递减“为事件
在定义域内单调递减“为事件 ,求事件
,求事件 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 .
. 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 ;
; 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数 在定义域内单调递增”为事件
在定义域内单调递增”为事件 ,求事件
,求事件