题目内容
已知定义在
上的函数
，满足对任意
，都有
成立，则
= 。
0或1006
解析试题分析：令a=b=0得：f（0）=f（0）+2f2（0）⇒f（0）=0；令a=0，b=1得：f（1）=f（0）+2f2（1）⇒f（1）=0或f（1）=
，令a=n，b=1得：f（n+1）=f（n）+2f2（1），当f（1）=0时，f（n+1）=f（n），则f（2012）=0；当f（1）=时，f（n+1）=f（n）+，构成一个等差数列，则f（2012）=f（1）+2011×=1006，则=0或1006
考点：本题考查了抽象函数的运用
点评：解答此类问题的关键是利用赋值法解决问题，属基础题．
练习册系列答案
相关题目
，若关于
的方程
有3个不同的实根，则实数
的取值范围是_________________．
，则函数
的定义域是 ．
= ；
，那么
。
在
上是增函数，则不等式
的解集是 .
，则
的值是 . 
、
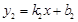的图象
、
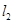相交于点P（－2，3），则不等式
＜
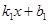的解集是 ．