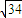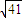题目内容
已知b＞0，设F1、F2是双曲线
-
=1的两个焦点，点P在此双曲线上，且
⊥
，|
•|
|=32，则b的值等于（ ）
| x2 |
| 9 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| PF1| |
| PF2 |
| A、4 | ||
| B、16 | ||
C、
| ||
D、
|
分析：由
⊥
，|
•|
|=32，知S△F1PF2=
|
| |
| =b2cot
，由此能求出b．
| PF1 |
| PF2 |
| PF1| |
| PF2 |
| 1 |
| 2 |
| PF1 |
| PF2 |
| 90° |
| 2 |
解答：解：∵
⊥
，|
•|
|=32，
∴S△F1PF2=
|
| |
| =b2cot
，
∴b2=16，b=4．
故选A．
| PF1 |
| PF2 |
| PF1| |
| PF2 |
∴S△F1PF2=
| 1 |
| 2 |
| PF1 |
| PF2 |
| 90° |
| 2 |
∴b2=16，b=4．
故选A．
点评：本题考查双曲线的简单性质，解题时要认真审题，注意公式的合理选用．
练习册系列答案
相关题目
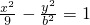的两个焦点，点P在此双曲线上，且
，
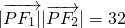，则b的值等于
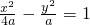的两个焦点，点尸在此双曲线上，且
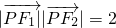，则a的值等于
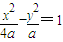的两个焦点，点尸在此双曲线上，且
，
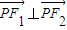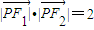，则a的值等于（ ）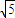
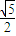
的两个焦点，点P在此双曲线上，且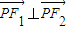
，
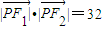，则b的值等于（ ）
