题目内容
| ∫ | 2 0 |
| 4-x2 |
π
π
．分析：利用微积分基本定理的几何意义即可得出．
解答：解：令y=
，画出图象：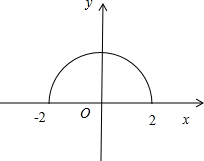
由微积分基本定理的几何意义可得：
=
×π×22=π．
故答案为π．
| 4-x2 |
由微积分基本定理的几何意义可得：
| ∫ | 2 0 |
| 4-x2 |
| 1 |
| 4 |
故答案为π．
点评：熟练掌握微积分基本定理的几何意义是解题的关键．
练习册系列答案
相关题目
计算
dx的结果是（ ）
| ∫ | 2 0 |
| 4-x2 |
| A、4π | ||
| B、2π | ||
| C、π | ||
D、
|
已知等比数列{an}，且a4+a6=
dx，则a5（a3+2a5+a7）的值为（ ）
| ∫ | 2 0 |
| 4-x2 |
| A、π2 | B、4 |
| C、π | D、-9π |