题目内容
设有两个命题:p:不等式(
)x+4>m>2x-x2对x∈R恒成立,q:f(x)=-(7-2m)x是R上的减函数;如果“p或q”为假命题,求实数m的取值范围.
| 1 | 3 |
分析:由不等式恒成立可得到m的范围,由符合函数的真假及指数函数的单调性,可求m的另一个范围,最后把复合命题“p或q”为假命题转化为p假而且q假,从而取交集的答案.
解答:解:不等式(
)x+4>m>2x-x2对x∈R恒成立,
等价于[(
)x+4]min>m>(2x-x2)max,
而[(
)x+4]min>4,(2x-x2)max=1
可得当p真:1<m≤4,则p假:m≤1或m>4;
f(x)=-(7-2m)x是R上的减函数,则(7-2m)>1
可得当q真:m<3,则q假:m≥3
“p或q”为假命题,表示p假而且q假
故实数m的取值范围为m>4
| 1 |
| 3 |
等价于[(
| 1 |
| 3 |
而[(
| 1 |
| 3 |
可得当p真:1<m≤4,则p假:m≤1或m>4;
f(x)=-(7-2m)x是R上的减函数,则(7-2m)>1
可得当q真:m<3,则q假:m≥3
“p或q”为假命题,表示p假而且q假
故实数m的取值范围为m>4
点评:本题考查复合命题的真假,涉及函数的最值问题及恒成立问题,属基础题.

练习册系列答案
相关题目
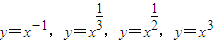 ,其中在R上是增函数的函数有3个.
,其中在R上是增函数的函数有3个.