题目内容
甲、乙两人进行围棋比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或下满6局时停止.设甲在每局中获胜的概率为p(p>| 1 |
| 2 |
| 5 |
| 9 |
(1)求p的值;
(2)设ξ表示比赛停止时已比赛的局数,求随机变量ξ的分布列和数学期望Eξ.
分析:(1)已知各局胜负相互独立,第二局比赛结束时比赛停止,包含甲连胜2局或乙连胜2局,写出甲连胜两局的概率和乙连胜两局的概率求和为
.解出关于P的方程.
(2)因为比赛进行到有一人比对方多2分或下满6局时停止,所以ξ的所有可能取值为2,4,6,而ξ=2已经做出概率,只要求出ξ=4或ξ=6时的概率即可,最后求出期望.
| 5 |
| 9 |
(2)因为比赛进行到有一人比对方多2分或下满6局时停止,所以ξ的所有可能取值为2,4,6,而ξ=2已经做出概率,只要求出ξ=4或ξ=6时的概率即可,最后求出期望.
解答:解:(1)当甲连胜2局或乙连胜2局时,
第二局比赛结束时比赛停止,故p2+(1-p)2=
,
解得p=
或p=
,又p>
,故p=
(2)依题意知ξ的所有可能取值为2,4,6,
设每两局比赛为一轮,则该轮结束时比赛停止的概率为
,
若该轮结束时比赛还将继续,则甲、乙在该轮中必是各得一分,
此时,该轮比赛结果对下轮比赛是否停止没有影响,从而有P(ξ=2)=
,P(ξ=4)=(1-
)×
=
,P(ξ=6)=(1-
)×(1-
)×1=
,
则随机变量ξ的分布列为:
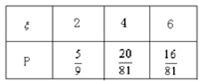
故Eξ=2×
+4×
+6×
=
.
第二局比赛结束时比赛停止,故p2+(1-p)2=
| 5 |
| 9 |
解得p=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
(2)依题意知ξ的所有可能取值为2,4,6,
设每两局比赛为一轮,则该轮结束时比赛停止的概率为
| 5 |
| 9 |
若该轮结束时比赛还将继续,则甲、乙在该轮中必是各得一分,
此时,该轮比赛结果对下轮比赛是否停止没有影响,从而有P(ξ=2)=
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
| 9 |
| 20 |
| 81 |
| 5 |
| 9 |
| 5 |
| 9 |
| 16 |
| 81 |
则随机变量ξ的分布列为:

故Eξ=2×
| 5 |
| 9 |
| 20 |
| 81 |
| 16 |
| 81 |
| 266 |
| 81 |
点评:求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,只要注意解题格式就问题不大.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
. 的值;
的值; 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量 .
. ),且各局胜负相互独立。已知第二局比赛结束时比赛停止的概率为
),且各局胜负相互独立。已知第二局比赛结束时比赛停止的概率为 。
。 ),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
. ),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
.