题目内容
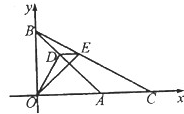
如图,
,
分别为x,y非负半轴上的单位向量,点C在x轴上且在点A的右侧,D、E分别为△ABC的边AB、BC上的点.若
与
+
共线.
与
共线,则
•
的值为( )
分析:由题意得E在∠A0B的平分线上.设E(m,m),根据
∥
得到D的坐标为(1-m,m),利用直线BE的方程算出C(
,0).由此可得
、
关于m的坐标形式,再由向量数量积的坐标公式即可算出
•
的值.
解答:解:根据题意,可得A(1,0),B(0,1),直线AB的方程为y=1-x,
∵
与
+
共线,|
|=|
|,
∴点E在∠A0B的平分线上,可得0E所在直线方程是y=x,
设E(m,m),由
与
共线,得D的纵坐标为m,
将y=m代入直线AB方程,得x=1-m,可得D(1-m,m),
∵B(0,1),E(m,m),
∴直线BE的方程为
=,化简得(m-1)x-my+m=0,
再令y=0得x=
,可得点C坐标为(
,0),
∴
=(
,-1),
=(1-m,m),可得
•
=
•(1-m)+(-1)•m=0.
故选:B
点评:本题以等腰三角形中的向量为载体,求两个向量的数量积.着重考查了向量的线性运算、向量的数量积公式与直线的方程等知识,考查了利用直角坐标系解决向量在几何问题中的应用的方法,属于中档题.
练习册系列答案
相关题目
 如图,
如图,
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案 如图所示,四边形OABP是平行四边形,过点P的直线与射线OA、OB分别相交于点M、N,若
如图所示,四边形OABP是平行四边形,过点P的直线与射线OA、OB分别相交于点M、N,若  如图,在?OABP中,过点P的直线与线段OA、OB分别交与点M、N,若
如图,在?OABP中,过点P的直线与线段OA、OB分别交与点M、N,若 (1)已知A(-1,2),B(2,8),
(1)已知A(-1,2),B(2,8), 如图,在平行四边形OABP中,过点P的直线与线段OA、OB分别相交于点M、N,若
如图,在平行四边形OABP中,过点P的直线与线段OA、OB分别相交于点M、N,若