题目内容
已知一次函数f(x)的图像关于直线x－y＝0对称的图像为C，且f[f(1)]＝－1，若点(n，
)(n∈N*)在曲线C上，并且a1＝1，
＝1(n≥2)．
(1)求f(x)的解析式及曲线C的方程；
(2)求数列{an)的通项公式；
(3)设Sn＝
，求
Sn的值．
答案：
解析：
解析：
|
解 (1)设f(x)＝kx＋b(k≠0)．则f[f(1)]＝k(k＋b)＋b＝k2＋kb＋b＝－1，即 k2＋kb＋b＋1＝0．① 又f－1(x)＝ f－1(n)－f－1(n－1)＝ 又f－1(n)－f－1(n－1)＝ 代入①得b＝－1．∴f(x)＝x－1．f－1(x)＝x＋1．曲线C的方程是x－y＋1＝0． (2)由(1)知当x＝n时，f－1(x)＝n＋1，故
(3)因为 Sn＝ |
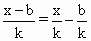是曲线C的解析式，因为点(n，
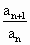)在曲线C上，所以，
＝1，
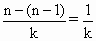，故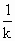
＝1，∴k＝1，
＝n＋1．而a1＝1，于是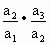
·…·
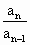＝2·3·4·…·n，即an＝n！．
，所以
，所以
．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，若f(x)是减函数，且f(1)=0，
x＋1
x－1