题目内容
在R上定义运算?:p?q=-
(p-c)(q-b)+4bc(b、c为实常数).记f1(x)=x2-2x,f2(x)=x-2b,x∈R.令f(x)=f1(x)?f2(x).
(Ⅰ)如果函数f(x)在x=1处有极值-
,试确定b、c的值;
(Ⅱ)记g(x)=|f′(x)|(-1≤x≤1)的最大值为M.若M≥k对任意的b、c 恒成立,试示k的最大值.
| 1 |
| 3 |
(Ⅰ)如果函数f(x)在x=1处有极值-
| 4 |
| 3 |
(Ⅱ)记g(x)=|f′(x)|(-1≤x≤1)的最大值为M.若M≥k对任意的b、c 恒成立,试示k的最大值.
分析:(I)由题意得到f(x)的解析式,求出f′(x)因为在x=1处有极值得到f(1)=-
,f′(1)=0求出b、c即可;
(II)根据题意得到g(x)的解析式,利用已知求出g(x)的最大值M,利用M≥k列出不等式求出k的取值范围即可.
| 4 |
| 3 |
(II)根据题意得到g(x)的解析式,利用已知求出g(x)的最大值M,利用M≥k列出不等式求出k的取值范围即可.
解答:解:(I)依题意:已知f1(x)=x2-2c,f2(x)=x-2b,f(x)=f1(x)f2(x).
得f(x)=-
x3+bx2+cx+bc,
解
得
或
.
若
,f(x)=-
x3+x2-x-1,
f′(x)=-x2+2x-1=-(x-1)2≤0,f(x)在R上单调递减,
在x=1处无极值;
若
,f(x)=-
x3-x2+3x-3,
f′(x)=-x2-2x+3=-(x-1)(x+3),直接讨论知,
f(x)在x=1处有极大值,所以
为所求.
(II)g(x)=|-(x-b)2+b2+c|.
若|b|>1,则f′(x)在[-1,1]是单调函数,
因为|b|>1,所以函数y=f′(x)的对称轴x=b位于区间[-1,1]之外,
所以f′(x)在[-1,1]上的最值在两端点处取得.
故M应是g(1)和g(-1)中较大的一个.
假设M≤2,则g(-1)=|-1-2b+c|≤2,
g(1)=|-1+2b+c|≤2,
将上述两式相加得:4≥|-1-2b+c|+|-1+2b+c|≥4|b|>4,导致矛盾,
所以M>2.
若|b|≤1,f′(x)在x=b∈[-1,1]取极值,
则M=max{|f′(-1)|,|f′(1)|,|f′(b)|},f′(b)-f′(±1)=(b?1)2.
若-1≤b<0,f′(1)≤f′(-1)≤f′(b)
M=max{|f/(1)|,|f/(b)|}≥
|f/(1)-f/(b)|=
(b-1)2>
;
若0≤b≤1,f′(-1)≤f′(1)≤f′(b),
M=max{|f′(-1)|,|f′(b)|}≥
|f/(-1)-f/(b)|=
(b+1)2≥
.
当b=0,c=
时,g(x)=|f/(x)|=|-x2+
|在[-1,1]上的最大值M=
.
所以,k的取值范围是(-∞,
].k的最大值为:
.
得f(x)=-
| 1 |
| 3 |
解
|
|
|
若
|
| 1 |
| 3 |
f′(x)=-x2+2x-1=-(x-1)2≤0,f(x)在R上单调递减,
在x=1处无极值;
若
|
| 1 |
| 3 |
f′(x)=-x2-2x+3=-(x-1)(x+3),直接讨论知,
f(x)在x=1处有极大值,所以
|
(II)g(x)=|-(x-b)2+b2+c|.
若|b|>1,则f′(x)在[-1,1]是单调函数,
因为|b|>1,所以函数y=f′(x)的对称轴x=b位于区间[-1,1]之外,
所以f′(x)在[-1,1]上的最值在两端点处取得.
故M应是g(1)和g(-1)中较大的一个.
假设M≤2,则g(-1)=|-1-2b+c|≤2,
g(1)=|-1+2b+c|≤2,
将上述两式相加得:4≥|-1-2b+c|+|-1+2b+c|≥4|b|>4,导致矛盾,
所以M>2.
若|b|≤1,f′(x)在x=b∈[-1,1]取极值,
则M=max{|f′(-1)|,|f′(1)|,|f′(b)|},f′(b)-f′(±1)=(b?1)2.
若-1≤b<0,f′(1)≤f′(-1)≤f′(b)
M=max{|f/(1)|,|f/(b)|}≥
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
若0≤b≤1,f′(-1)≤f′(1)≤f′(b),
M=max{|f′(-1)|,|f′(b)|}≥
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当b=0,c=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以,k的取值范围是(-∞,
| 1 |
| 2 |
| 1 |
| 2 |
点评:本小题主要考查导数几何意义、导数研究函数极值、函数恒成立问题、绝对值不等式的性质等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
相关题目
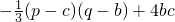 (b、c为实常数).记
(b、c为实常数).记 ,f2(x)=x-2b,x∈R.令f(x)=f1(x)?f2(x).
,f2(x)=x-2b,x∈R.令f(x)=f1(x)?f2(x). ,试确定b、c的值;
,试确定b、c的值; :p
:p q=-
q=- (p-c)(q-b)+4bc(b、c∈R是常数)。记f1(x)=x2-2c,f2(x)=x-2b,x∈R,令f(x)=f1(x)
(p-c)(q-b)+4bc(b、c∈R是常数)。记f1(x)=x2-2c,f2(x)=x-2b,x∈R,令f(x)=f1(x) f2(x)。
f2(x)。 ,试确定b、c的值;
,试确定b、c的值;