题目内容
sin(65°-x)cos(x-20°)+cos(65°-x)cos(110°-x)的值为( )A.
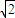
B.

C.

D.
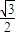
【答案】分析:先把cos(110°-x)变为cos[90°-(x-20°)],然后利用诱导公式化简为sin(x-20°),则利用两角和与差的正弦公式的逆运算得到特殊角的三角函数值,求出值即可.
解答:解析:原式=sin(65°-x)cos(x-20°)+cos(65°-x)•cos[90°-(x-20°)]
=sin(65°-x)cos(x-20°)+cos(65°-x)sin(x-20°)
=sin[(65°-x)+(x-20°)]=sin45°=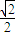 .
.
故选B
点评:考查学生会进行角度的变换,灵活运用两角和与差的正弦函数公式进行化简求值,会利用诱导公式及特殊角的三角函数值进行化简求值.
解答:解析:原式=sin(65°-x)cos(x-20°)+cos(65°-x)•cos[90°-(x-20°)]
=sin(65°-x)cos(x-20°)+cos(65°-x)sin(x-20°)
=sin[(65°-x)+(x-20°)]=sin45°=
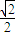 .
.故选B
点评:考查学生会进行角度的变换,灵活运用两角和与差的正弦函数公式进行化简求值,会利用诱导公式及特殊角的三角函数值进行化简求值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目