题目内容
19．解不等式：x4+2x3-x-2＞0．分析 通过因式分解将不等式转化为不等式组解出即可．
解答 解：∵x4+2x3-x-2＞0，
∴x3（x+2）-（x+2）＞0，
∴（x+2）（x3-1）＞0，
∴$\left\{\begin{array}{l}{x+2＞0}\\{{x}^{3}-1＞0}\end{array}\right.$或$\left\{\begin{array}{l}{x+2＜0}\\{{x}^{3}-1＜0}\end{array}\right.$，
解得：x＞1或x＜-2．
点评 本题考查了解不等式问题，因式分解是常用方法之一，本题是一道基础题．
练习册系列答案
相关题目
2．
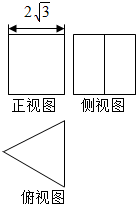一个体积为12$\sqrt{3}$的正三棱柱（底面为正三角形，且侧棱垂直于底面的棱柱）的三视图如图所示，则该三棱柱的侧视图的面积为（ ）
一个体积为12$\sqrt{3}$的正三棱柱（底面为正三角形，且侧棱垂直于底面的棱柱）的三视图如图所示，则该三棱柱的侧视图的面积为（ ）| A． | 6$\sqrt{3}$ | B． | 8 | C． | 8$\sqrt{3}$ | D． | 12 |
11．下列结论正确的是（ ）
| A． | 已知向量$\vec a，\vec b$为非零向量，则“$\vec a，\vec b$的夹角为钝角”的充要条件是“$\vec a•\vec b＜0$” | |
| B． | 对于命题p和q，“p且q为真命题”的必要而不充分条件是“p或q为真命题” | |
| C． | 命题“若x2=1，则x=1或x=-1”的逆否命题为“若x≠1或x≠-1，则x2≠1” | |
| D． | 若命题p：?x∈R，x2-x+1＜0，则￢p：?x∈R，x2-x+1＞0 |
8．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，左顶点为A，点B（0，b），若线段AF1（不含端点）上存在点P，使得以PF2为直径的圆经过点B，则双曲线C的离心率的取值范围是（ ）
| A． | （1，$\frac{1+\sqrt{5}}{2}$） | B． | （$\frac{1+\sqrt{5}}{2}$，+∞） | C． | （$\sqrt{2}$，$\frac{1+\sqrt{5}}{2}$） | D． | （$\sqrt{2}$，+∞） |