题目内容
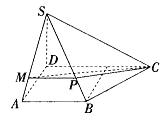
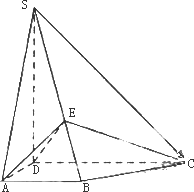
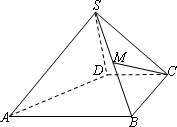
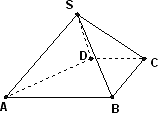
如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=![]() a(0<
a(0<![]() ≦1). w.w.w.k.s.5.u.c.o.m
≦1). w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅰ)求证:对任意的![]()
![]() (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C,求![]() 的值。
的值。
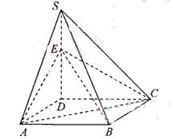
(Ⅰ) 略(Ⅱ)![]()
解析:
本小题主要考察空间直线与直线、直线与平面的位置关系和二面角等基础知识,考查空间想象能力、推理论证能力和运算求解能力。(满分12分)
(Ⅰ)连接BD,由底面是正方形可得AC![]() BD。
BD。
![]() SD
SD![]() 平面ABCD,
平面ABCD,![]() BD是BE在平面ABCD上的射影,
BD是BE在平面ABCD上的射影,
由三垂线定理得AC![]() BE.
BE.
(II) ![]() SD
SD![]() 平面ABCD,CD
平面ABCD,CD![]() 平面ABCD,
平面ABCD,![]() SD
SD![]() CD.
CD.
又底面ABCD是正方形,![]() CD
CD![]() AD,又SD
AD,又SD![]() AD=D,
AD=D,![]() CD
CD![]() 平面SAD。
平面SAD。
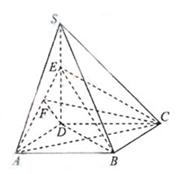
过点D在平面SAD内做DF![]() AE于F,连接CF,则CF
AE于F,连接CF,则CF![]() AE,
AE,
故![]() CFD是二面角C-AE-D 的平面角,即
CFD是二面角C-AE-D 的平面角,即![]() CFD=60°
CFD=60°
在Rt△ADE中,![]() AD=
AD=![]() , DE=
, DE= ![]() , AE=
, AE=![]()
![]() 。
。
于是,DF=![]()
在Rt△CDF中,由![]() cot60°=
cot60°=![]()
得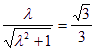 , 即
, 即![]() =3
=3![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
![]() , 解得
, 解得![]() =
=![]()

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目