题目内容
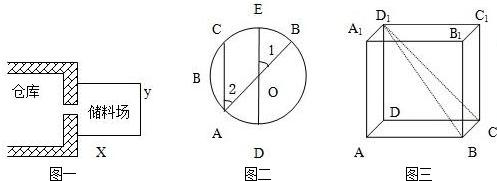
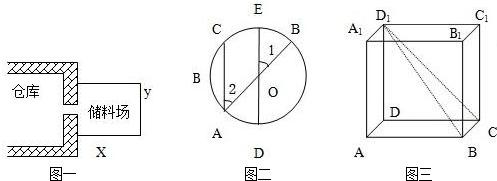
(1)某工厂准备在仓库的一侧建立一个矩形储料场(如图1),现有50米长的铁丝网,如果用它来围成这个储料场,那么长和宽各是多少时,这个储料场的面积最大?并求出这个最大的面积.(2)如图2,已知AB、DE是圆O的直径,AC是弦,AC∥DE,求证CE=EB.
(3)如图3所示的棱长为a的正方体中:①求CD1和AB所成的角的度数;②求∠B1BD1的正弦值.

【答案】分析:(1)由图可知储料场是个矩形,设出其长为x宽为y,根据条件2x+y=50,用y表示出x,然后用配方法求出其最大值;
(2)根据中位线定理可得EB= CB,然后再结合条件CB=CE+EB,进行证明;
CB,然后再结合条件CB=CE+EB,进行证明;
(3)①CD1和AB所成的角等于∠D1CD,是个等腰三角形进而求解;②利用正弦三角函数的定义和性质进行求解.
解答:(1)解:设矩形储料场的长为x宽为y,则因其一面靠墙,所以应有2x+y=50,即y=50-2x,设储料场的面积为S,
则S=xy=x(50-2x)
=-2x2+50x
=-2(x-12.5)2+312.5
∴当x=12.5时,储料场的面积最,S=312.5米2此时y=25米.
(2)解:证:∵AC∥DE,∴∠1=∠2.
∴EB= CB,CB=2EB
CB,CB=2EB
但CB=CE+EB,
∴2EB=CE+EB,CE=EB,CE=EB.
(3)解:①CD1和AB所成的角等于∠D1CD,
∵△D1CD是等腰三角形,∴∠D1CD=45°.
②∵D1B1= a,D1B=
a,D1B= a,
a,
∴ .
.
点评:(1)是一道实际应用题,考查二次函数的最值问题,主要配方法是高考常用的方法;
(2)考查圆内简单的几何关系,利用三角形中位线定理进行求解;
(3)是一道简单的立体几何问题,解题的关键是找出所求的角,是一道基础题.
(2)根据中位线定理可得EB=
 CB,然后再结合条件CB=CE+EB,进行证明;
CB,然后再结合条件CB=CE+EB,进行证明;(3)①CD1和AB所成的角等于∠D1CD,是个等腰三角形进而求解;②利用正弦三角函数的定义和性质进行求解.
解答:(1)解:设矩形储料场的长为x宽为y,则因其一面靠墙,所以应有2x+y=50,即y=50-2x,设储料场的面积为S,
则S=xy=x(50-2x)
=-2x2+50x
=-2(x-12.5)2+312.5
∴当x=12.5时,储料场的面积最,S=312.5米2此时y=25米.
(2)解:证:∵AC∥DE,∴∠1=∠2.
∴EB=
 CB,CB=2EB
CB,CB=2EB但CB=CE+EB,
∴2EB=CE+EB,CE=EB,CE=EB.
(3)解:①CD1和AB所成的角等于∠D1CD,
∵△D1CD是等腰三角形,∴∠D1CD=45°.
②∵D1B1=
 a,D1B=
a,D1B= a,
a,∴
 .
.点评:(1)是一道实际应用题,考查二次函数的最值问题,主要配方法是高考常用的方法;
(2)考查圆内简单的几何关系,利用三角形中位线定理进行求解;
(3)是一道简单的立体几何问题,解题的关键是找出所求的角,是一道基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 某先生居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率,如图.( 例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为
某先生居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率,如图.( 例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为 如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,设AB=y km,并在公路同侧建造边长为x km的正方形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°.
如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,设AB=y km,并在公路同侧建造边长为x km的正方形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°.