题目内容
已知函数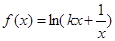 ,(
,(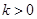 )在
)在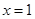 处取得最小值.
处取得最小值.
(Ⅰ)求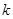 的值;
的值;
(Ⅱ)若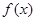 在
在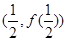 处的切线方程为
处的切线方程为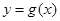 ,求证:当
,求证:当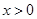 时,曲线
时,曲线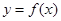 不可能在直线
不可能在直线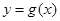 的下方;
的下方;
(Ⅲ)若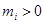 ,(
,(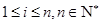 )且
)且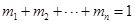 ,试比较
,试比较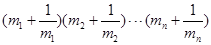 与
与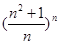 的大小,并证明你的结论.
的大小,并证明你的结论.
【答案】
(Ⅰ)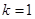 ;(Ⅱ)详见解析;(Ⅲ)详见解析.
;(Ⅱ)详见解析;(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)导数法,先求导数,由条件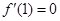 ,得出
,得出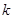 的值,再令
的值,再令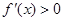 或
或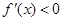 ,判断函数的单调区间;(Ⅱ)导数法,构造新函数
,判断函数的单调区间;(Ⅱ)导数法,构造新函数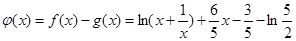 ,再用导数法,证明
,再用导数法,证明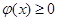
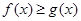 在
在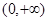 恒成立,从而得出结论;(Ⅲ)用导数的几何意义,得出直线方程
恒成立,从而得出结论;(Ⅲ)用导数的几何意义,得出直线方程 ,在用导数法证明
,在用导数法证明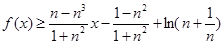 .
.
试题解析:(Ⅰ)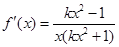 ,由已知得
,由已知得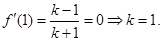 ,
(3分)
,
(3分)
当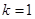 时
时 ,此时
,此时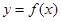 在
在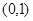 单调递减,在
单调递减,在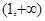 单调递增,
单调递增,
(Ⅱ) ,
,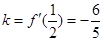 ,
,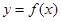 在
在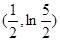 的切线方程为
的切线方程为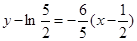 ,
,
即 .
(6分)
.
(6分)
当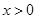 时,曲线
时,曲线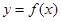 不可能在直线
不可能在直线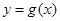 的下方
的下方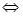
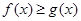 在
在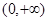 恒成立,
恒成立,
令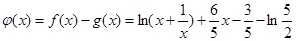 ,
,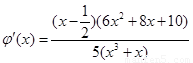 ,
,
当 ,
,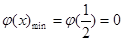 ,
,
即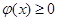
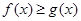 在
在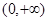 恒成立,
恒成立,
所以当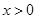 时,曲线
时,曲线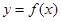 不可能在直线
不可能在直线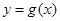 的下方,
(9分)
的下方,
(9分)
(Ⅲ) ,
,
先求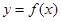 在
在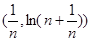 处的切线方程,
处的切线方程,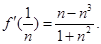 故
故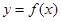 在
在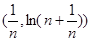 的切线方程为
的切线方程为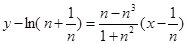 ,即
,即 ,
,
下先证明 ,
,
令
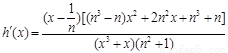 ,
,
当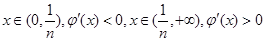 ,
,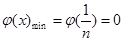
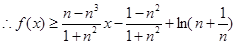

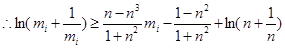
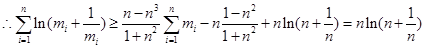
 .
(14分)
.
(14分)
考点:导数的运算法则,利用导数研究函数的极值,不等式的证明等知识.

练习册系列答案
相关题目
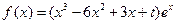 ,
,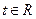 .依次在
.依次在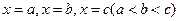 处取到极值.
处取到极值.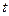 的取值范围;
的取值范围;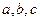 成等差数列,求
成等差数列,求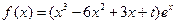 ,
,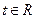 .依次在
.依次在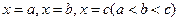 处取到极值.
处取到极值.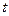 的取值范围;
的取值范围;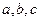 成等差数列,求
成等差数列,求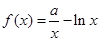 .
.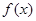 在
在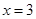 处取得极值,求实数
处取得极值,求实数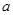 的值;
的值;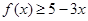 恒成立,求实数
恒成立,求实数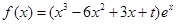 ,
,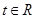 .依次在
.依次在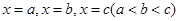 处取到极值.
处取到极值.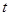 的取值范围;
的取值范围;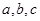 成等差数列,求
成等差数列,求