题目内容
收集本地区教育储蓄信息,有一公民的储蓄方式为:第一年末存入a1元,以后每年末存入的数目均比上一年增加d(d>0)元,因此,历年所存入的教育储蓄金数目a1,a2,…是一个公差为d的等差数列,与此同时,政府给予优惠的计息政策,不仅采用固定利率,而且计算复利,也不征利息税.这就是说,如果固定年利率为p(p>0),那么,在第n年末,第一年所存入的储蓄金就变为a1(1+p)n-1,第二年所存入的储蓄金就变为a2(1+p)n-2,…,以Wn表示到第n年末所累计的储蓄金总额.(1)写出Wn与Wn-1(n≥2)的递推关系式;
(2)是否存在数列{An},{Bn}使Wn=An+Bn,其中{An}是一个等比数列,{Bn}是一个等差数列,说明你的理由.
【答案】分析:(1)根据第n年末,第一年所存入的储蓄金就变为a1(1+p)n-1,第二年所存入的储蓄金就变为a2(1+p)n-2,…,可求Wn与Wn-1(n≥2)的递推关系式;
(2)根据(1)的结论,反复使用,可得Wn=a1(1+p)n-1+a2(1+p)n-2+…+an-1(1+p)+an,两边同乘以(1+p),利用错位相减法求和,结合等差数列等比数列的定义,可得结论.
解答:解:(1)根据第n年末,第一年所存入的储蓄金就变为a1(1+p)n-1,第二年所存入的储蓄金就变为a2(1+p)n-2,…,可知W1=a1,W2=W1(1+p)+a2,Wn=Wn-1(1+p)+an(n≥2)…4分
(2)W1=a1,Wn=Wn-1(1+p)+an,对n≥2反复使用上述关系式,
得Wn=Wn-1(1+p)+an=[Wn-2(1+p)+an-1](1+p)+an=Wn-2(1+p)2+(1+p)an-1+an
…=W1(1+p)n-1+a2(1+p)n-2+…+an-1(1+p)+anWn=a1(1+p)n-1+a2(1+p)n-2+…+an-1(1+p)+an①…6分
(1+p)Wn=a1(1+p)n+a2(1+p)n-1+…+an-1(1+p)2+an(1+p)②
②-①pWn=a1(1+p)n+d(1+p)n-1+d(1+p)n-2…+d(1+p)-an=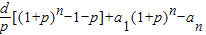 …8分
…8分
即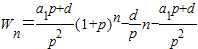
如果记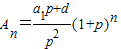 ,
,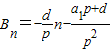 ,…10分
,…10分
则Tn=An+Bn.
其中{An}是以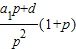 为首项,以(1+p)(p>0)为公比的等比数列;{Bn}是以
为首项,以(1+p)(p>0)为公比的等比数列;{Bn}是以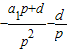 为首项,
为首项,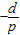 为公差的等差数列.…14分
为公差的等差数列.…14分
点评:本题的考点是数列的应用,解题的关键是从实际问题中抽象出数列模型,再利用数列的求和方法进行求和.判断一个数列是否是等差(比)数列,我们有如下办法:①定义法②通项公式法(如本题)③前n项和公式法④等差(比)中项法.
(2)根据(1)的结论,反复使用,可得Wn=a1(1+p)n-1+a2(1+p)n-2+…+an-1(1+p)+an,两边同乘以(1+p),利用错位相减法求和,结合等差数列等比数列的定义,可得结论.
解答:解:(1)根据第n年末,第一年所存入的储蓄金就变为a1(1+p)n-1,第二年所存入的储蓄金就变为a2(1+p)n-2,…,可知W1=a1,W2=W1(1+p)+a2,Wn=Wn-1(1+p)+an(n≥2)…4分
(2)W1=a1,Wn=Wn-1(1+p)+an,对n≥2反复使用上述关系式,
得Wn=Wn-1(1+p)+an=[Wn-2(1+p)+an-1](1+p)+an=Wn-2(1+p)2+(1+p)an-1+an
…=W1(1+p)n-1+a2(1+p)n-2+…+an-1(1+p)+anWn=a1(1+p)n-1+a2(1+p)n-2+…+an-1(1+p)+an①…6分
(1+p)Wn=a1(1+p)n+a2(1+p)n-1+…+an-1(1+p)2+an(1+p)②
②-①pWn=a1(1+p)n+d(1+p)n-1+d(1+p)n-2…+d(1+p)-an=
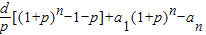 …8分
…8分即
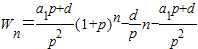
如果记
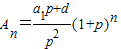 ,
,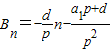 ,…10分
,…10分则Tn=An+Bn.
其中{An}是以
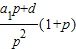 为首项,以(1+p)(p>0)为公比的等比数列;{Bn}是以
为首项,以(1+p)(p>0)为公比的等比数列;{Bn}是以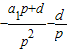 为首项,
为首项,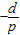 为公差的等差数列.…14分
为公差的等差数列.…14分点评:本题的考点是数列的应用,解题的关键是从实际问题中抽象出数列模型,再利用数列的求和方法进行求和.判断一个数列是否是等差(比)数列,我们有如下办法:①定义法②通项公式法(如本题)③前n项和公式法④等差(比)中项法.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目