题目内容
已知x2-mx+n=0的两根为α，β，且1＜α＜2＜β，则m2+n2的取值范围是（ ）
| A、[12，+∞） | B、（12，+∞） | C、[13，+∞） | D、（13，+∞） |
分析：结合二次方程相应的二次函数的图象，令f（1）＞0，f（2）＜0，列出不等式组，画出不等式表示的可行域，m2+n2表示可行域内的点到原点的距离，结合图求出m2+n2的范围．
解答：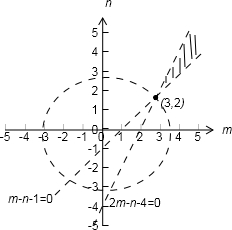
解：令f（x）=x2-mx+n
∵x2-mx+n=0的两根为α，β，且1＜α＜2＜β
∴
画出不等式表示的平面区域
m2+n2表示可行域内的点到原点的距离的平方，由图知当圆经过（3，2）时最小，
∴m2+n2＞32+22=13
故选D
解：令f（x）=x2-mx+n∵x2-mx+n=0的两根为α，β，且1＜α＜2＜β
∴
|
画出不等式表示的平面区域
m2+n2表示可行域内的点到原点的距离的平方，由图知当圆经过（3，2）时最小，
∴m2+n2＞32+22=13
故选D
点评：本题考查一元二次方程的根的分布，结合二次函数的图象从判别式、对称轴与区间的位置、区间端点值的符号考虑、考查线性规划求最值．
练习册系列答案
相关题目