题目内容
若正数 满足
满足 ,则
,则 的最小值是___________.
的最小值是___________.
5
解析试题分析: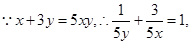 所以3x+4y=(3x+4y)
所以3x+4y=(3x+4y)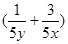 =
=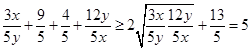
考点:1.基本不等式的应用.2.构造等式一边是1.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
题目内容
若正数 满足
满足 ,则
,则 的最小值是___________.
的最小值是___________.
5
解析试题分析: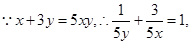 所以3x+4y=(3x+4y)
所以3x+4y=(3x+4y)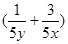 =
=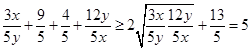
考点:1.基本不等式的应用.2.构造等式一边是1.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案