题目内容
 某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165],第2组[165,170],第3组[170,175],第4组[175,180),第5组[180,185),得到的频率分布直方图如图所示.
某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165],第2组[165,170],第3组[170,175],第4组[175,180),第5组[180,185),得到的频率分布直方图如图所示.(1)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少学生进入第二轮面试?
(2)在(1)的前提下,高校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.
(3)根据频率直方图,求笔试成绩的中位数.
分析:(1)求出第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,得到第3、4、5组分别抽取的人数.
(2)设在这6名学生中随机抽取2名学生的事件接受甲考官的面试事件A,第4组至少有一名学生被甲考官面试为事件B,事件A包含的基本事件数为
+
,事件B包含的基本事件数为
,由此能求出第4组至少有一名学生被甲考官面试的概率.
(3)第一、二两组的频率和为0.4,第三组的频率为0.3,所以中位数落在第三组,由此能求出笔试成绩的中位数.
(2)设在这6名学生中随机抽取2名学生的事件接受甲考官的面试事件A,第4组至少有一名学生被甲考官面试为事件B,事件A包含的基本事件数为
| C | 2 2 |
| C | 1 2 |
| C | 1 4 |
| C | 2 6 |
(3)第一、二两组的频率和为0.4,第三组的频率为0.3,所以中位数落在第三组,由此能求出笔试成绩的中位数.
解答:解:(1)第3组的人数为0.3×100=30,
第4组的人数为0.2×100=20,
第5组的人数为0.1×100=10.…(2分)
因为第3、4、5组共有60名学生,
所以利用分层抽样在60名学生中抽取6名学生(3分)
每组抽取的人数分别为第3组:
×6=3,
第4组:
×6=2,第5组:
×6=1,
所以第3、4、5组分别抽取3人、2人、1人.…(5分)
(2)设在这6名学生中随机抽取2名学生的事件接受甲考官的面试事件A,
第4组至少有一名学生被甲考官面试为事件B,…(6分)
事件A包含的基本事件数为
+
…(7分)
事件B包含的基本事件数为
…(8分)
所以第4组至少有一名学生被甲考官面试的概率为
p=
=
=
.…(10分)
(3)第一、二两组的频率和为0.4,
第三组的频率为0.3,
所以中位数落在第三组.(11分)
设中位数距离170为x,则
=
,解得x=1
…(13分)
故笔试成绩的中位数为171
.(取近似值不扣分)…(14分)
第4组的人数为0.2×100=20,
第5组的人数为0.1×100=10.…(2分)
因为第3、4、5组共有60名学生,
所以利用分层抽样在60名学生中抽取6名学生(3分)
每组抽取的人数分别为第3组:
| 30 |
| 60 |
第4组:
| 20 |
| 60 |
| 10 |
| 60 |
所以第3、4、5组分别抽取3人、2人、1人.…(5分)
(2)设在这6名学生中随机抽取2名学生的事件接受甲考官的面试事件A,
第4组至少有一名学生被甲考官面试为事件B,…(6分)
事件A包含的基本事件数为
| C | 2 2 |
| C | 1 2 |
| C | 1 4 |
事件B包含的基本事件数为
| C | 2 6 |
所以第4组至少有一名学生被甲考官面试的概率为
p=
| ||||||
|
| 9 |
| 15 |
| 3 |
| 5 |
(3)第一、二两组的频率和为0.4,
第三组的频率为0.3,
所以中位数落在第三组.(11分)
设中位数距离170为x,则
| 0.1 |
| 0.3 |
| x |
| 5 |
| 2 |
| 3 |
故笔试成绩的中位数为171
| 2 |
| 3 |
点评:本题考查频率分布直方图的应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
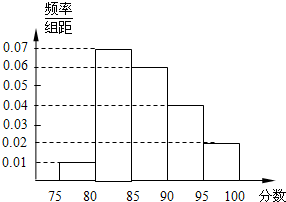 某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.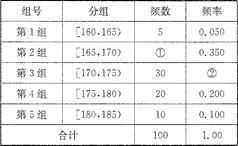
 名学生被考官D面试,求
名学生被考官D面试,求