题目内容
在△ABC中,BD为∠ABC的平分线,AB=3,BC=2,AC=
,则sin∠ABD=( )
| 7 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:由余弦定理表示出cos∠ABC,把已知的三角形的三边代入求出cos∠ABC的值,再由∠ABC的范围,利用特殊角的三角函数值求出∠ABC的度数,又BD为∠ABC的平分线,利用角平分线的定义求出∠ABD的度数,即可求出sin∠ABD的值.
解答:解:∵AB=3,BC=2,AC=
,
∴根据余弦定理得:cos∠ABC=
=
,又∠ABC为三角形的内角,
∴∠ABC=60°,又BD为∠ABC的平分线,
∴∠ABD=
∠ABC=30°,
则sin∠ABD=sin30°=
.
故选A.
| 7 |
∴根据余弦定理得:cos∠ABC=
| 9+4-7 |
| 2•3•2 |
| 1 |
| 2 |
∴∠ABC=60°,又BD为∠ABC的平分线,
∴∠ABD=
| 1 |
| 2 |
则sin∠ABD=sin30°=
| 1 |
| 2 |
故选A.
点评:此题考查了余弦定理,特殊角的三角函数值,以及角平分线的定义,根据余弦定理及特殊角的三角函数值求出∠ABC的度数是解本题的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
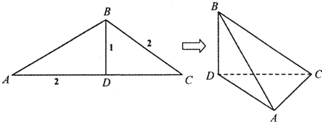 如图,在△ABC中,BD为AC边上的高,BD=1,BC=AD=2,沿BD将△ABD翻折,使得∠ADC=30°,得到几何体B-ACD.
如图,在△ABC中,BD为AC边上的高,BD=1,BC=AD=2,沿BD将△ABD翻折,使得∠ADC=30°,得到几何体B-ACD.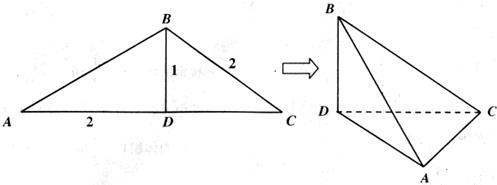 如图,在△ABC中,BD为AC边上的高,BD=1,BC=AD=2,沿BD将△ABD翻折,使得∠ADC=30°,得到几何体B-ACD.
如图,在△ABC中,BD为AC边上的高,BD=1,BC=AD=2,沿BD将△ABD翻折,使得∠ADC=30°,得到几何体B-ACD.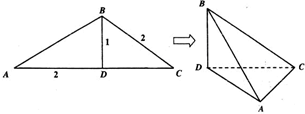 如图,在△ABC中,BD为AC边上的高,BD=1,BC=AD=2,沿BD将△ABD翻折,使得∠ADC=30°,得几何体B-ACD
如图,在△ABC中,BD为AC边上的高,BD=1,BC=AD=2,沿BD将△ABD翻折,使得∠ADC=30°,得几何体B-ACD