题目内容
 如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数y=Asin(ωx+
如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数y=Asin(ωx+| 2π | 3 |
(1)求曲线段FBC的解析式,并求∠DOE的大小;
(2)若南湖管理处要在圆弧大道所对应的扇形DOE区域内修建如图所示的水上乐园PQMN,问点P落在圆弧DE上何处时,水上乐园的面积最大?
分析:(1)根据图象,确定函数的最大值,周期,从而可得曲线段FBC的解析式,当x=0时,y=|OC|=
,从而可求∠DOE的大小;
(2)由(1)知OD=3,连接OP,设∠POE=θ,0<θ<
,进而可表示水上乐园PQMN面积,化简函数,根据角的范围,即可求得结论.
3
| ||
| 2 |
(2)由(1)知OD=3,连接OP,设∠POE=θ,0<θ<
| π |
| 3 |
解答:解:(1)由图象知A=3,
=3,∴T=12=
,∴ω=
,
∴曲线段FBC的解析式为y=3sin(
x+
),(-4≤x≤0).…(3分)
当x=0时,y=|OC|=
,
又CD=
,∴∠COD=
,∴∠DOE=
.…(5分)
(2)由(1)知OD=3,连接OP,设∠POE=θ,0<θ<
,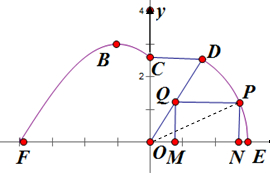
△PON中,OP=3,PN=3sinθ,ON=3cosθ,…(6分)
△QOM中,QM=PN=3sinθ,OM=
sinθ,从而MN=3cosθ-
sinθ,…(8分)
则水上乐园PQMN面积S=3sinθ(3cosθ-
sinθ)=9sinθcosθ-3
sin2θ=
sin2θ-3
×
=
sin2θ+
cos2θ-
=3
sin(2θ+
)-
,
∵0<θ<
,∴当2θ+
=
,θ=
时,Smax=
.…(11分)
答:(1)曲线段FBC的解析式为y=3sin(
x+
),(-4≤x≤0),∠DOE=
;
(2)当P点在圆弧DE中点时,水上乐园的面积最大,最大值为
km2.…(12分)
| T |
| 4 |
| 2π |
| ω |
| π |
| 6 |
∴曲线段FBC的解析式为y=3sin(
| π |
| 6 |
| 2π |
| 3 |
当x=0时,y=|OC|=
3
| ||
| 2 |
又CD=
| 3 |
| 2 |
| π |
| 6 |
| π |
| 3 |
(2)由(1)知OD=3,连接OP,设∠POE=θ,0<θ<
| π |
| 3 |

△PON中,OP=3,PN=3sinθ,ON=3cosθ,…(6分)
△QOM中,QM=PN=3sinθ,OM=
| 3 |
| 3 |
则水上乐园PQMN面积S=3sinθ(3cosθ-
| 3 |
| 3 |
| 9 |
| 2 |
| 3 |
| 1-cos2θ |
| 2 |
=
| 9 |
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
| 3 |
| π |
| 6 |
3
| ||
| 2 |
∵0<θ<
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
3
| ||
| 2 |
答:(1)曲线段FBC的解析式为y=3sin(
| π |
| 6 |
| 2π |
| 3 |
| π |
| 3 |
(2)当P点在圆弧DE中点时,水上乐园的面积最大,最大值为
3
| ||
| 2 |
点评:本题考查三角函数解析式的求解,考查四边形面积的计算,考查三角函数的化简,确定函数解析式是关键.

练习册系列答案
相关题目
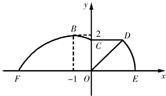 如图,某市准备在道路EF的一侧修建一条运动比赛道,赛道的前一部分为曲线段FBC,该曲线段是函数
如图,某市准备在道路EF的一侧修建一条运动比赛道,赛道的前一部分为曲线段FBC,该曲线段是函数
 (A>0,ω>0),x∈[﹣4,0]时的图象,且图象的最高点为B(﹣1,2).赛道的中间部分为长
(A>0,ω>0),x∈[﹣4,0]时的图象,且图象的最高点为B(﹣1,2).赛道的中间部分为长 千米的直线跑道CD,且CD∥EF.赛道的后一部分是以O为圆心的一段圆弧
千米的直线跑道CD,且CD∥EF.赛道的后一部分是以O为圆心的一段圆弧 .
. 上,且∠POE=θ,求当“矩形草坪”的面积取最大值时θ的值.
上,且∠POE=θ,求当“矩形草坪”的面积取最大值时θ的值.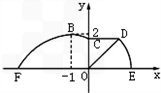

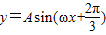 (A>0,ω>0),x∈[-4,0]时的图象,且图象的最高点为B(-1,2).赛道的中间部分为长
(A>0,ω>0),x∈[-4,0]时的图象,且图象的最高点为B(-1,2).赛道的中间部分为长 千米的直线跑道CD,且CD∥EF.赛道的后一部分是以O为圆心的一段圆弧
千米的直线跑道CD,且CD∥EF.赛道的后一部分是以O为圆心的一段圆弧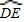 .
. 上,且∠POE=θ,求当“矩形草坪”的面积取最大值时θ的值.
上,且∠POE=θ,求当“矩形草坪”的面积取最大值时θ的值.