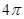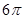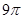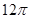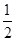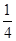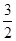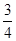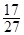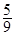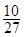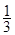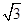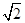题目内容
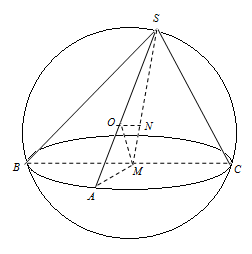
(5分)(2011•重庆)高为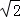 的四棱锥S﹣ABCD的底面是边长为1的正方形,点S,A,B,C,D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为( )
的四棱锥S﹣ABCD的底面是边长为1的正方形,点S,A,B,C,D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为( )
A.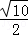 | B.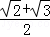 | C.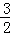 | D.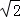 |
A
解析试题分析:由题意可知ABCD 是小圆,对角线长为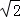 ,四棱锥的高为
,四棱锥的高为 ,推出高就是四棱锥的一条侧棱,最长的侧棱就是球的直径,然后利用勾股定理求出底面ABCD的中心与顶点S之间的距离.
,推出高就是四棱锥的一条侧棱,最长的侧棱就是球的直径,然后利用勾股定理求出底面ABCD的中心与顶点S之间的距离.
解:由题意可知ABCD 是小圆,对角线长为 ,四棱锥的高为
,四棱锥的高为 ,点S,A,B,C,D均在半径为1的同一球面上,球的直径为2,所以四棱锥的一条侧棱垂直底面的一个顶点,最长的侧棱就是直径,所以底面ABCD的中心与顶点S之间的距离为:
,点S,A,B,C,D均在半径为1的同一球面上,球的直径为2,所以四棱锥的一条侧棱垂直底面的一个顶点,最长的侧棱就是直径,所以底面ABCD的中心与顶点S之间的距离为: =
=
故选A
点评:本题是基础题,考查球的内接多面体的知识,能够正确推出四棱锥的一条侧棱垂直底面的一个顶点,最长的侧棱就是直径是本题的关键,考查逻辑推理能力,计算能力.

练习册系列答案
相关题目
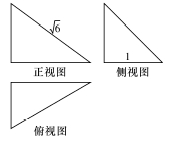
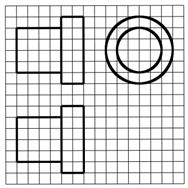
某向何体的三视图如图所示,则该几何体的体积为( )
A.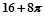 | B.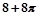 | C.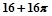 | D.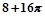 |
如图是一个几何体的三视图(侧视图中的弧线是半圆),则该几何体的表面积是( )
A.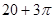 | B.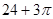 | C.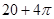 | D.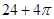 |
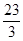
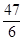
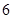
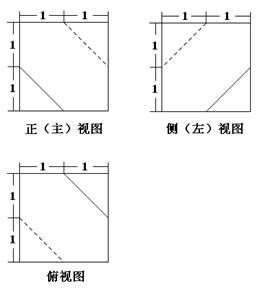
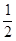 cm3
cm3 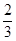 cm3
cm3 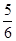 cm3
cm3 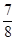 cm3
cm3 
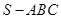 的四个顶点都在球面上,SA是球的直径,
的四个顶点都在球面上,SA是球的直径, ,
,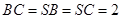 ,则该球的表面积为( )
,则该球的表面积为( )