题目内容
设直线(L)的参数方程是
|
|
分析:首先题中的直线方程及椭圆方程都是参数方程的形式,需要消去参数化简为一般方程,然后求公共点问题,考虑到联立方程式由求判别式的方法求取值范围即可得到答案.
解答:解:对于直线(L)
消去参数,得一般方程y=mx+b;
对于椭圆(E)
消去参数,得一般方程
+y2=1.:
消去y,整理得(1+a2m2)x2+2(a2mb-1)x+a2b2-a2+1=0.
(L)、(E)有交点的条件是上式的判别式≥0,即(a2mb-1)2-(1+a2m2)(a2b2-a2+1)≥0.
化简并约去a2得(a2-1)m2-2bm+(1-b2)≥0.对任意m的值,要使这个式子永远成立,条件是
(1)
或(2)
解得(1)
或(2)
或(1)、(2)合写成:
即所求的条件.
故答案为
.
|
对于椭圆(E)
|
| (x-1)2 |
| a2 |
消去y,整理得(1+a2m2)x2+2(a2mb-1)x+a2b2-a2+1=0.
(L)、(E)有交点的条件是上式的判别式≥0,即(a2mb-1)2-(1+a2m2)(a2b2-a2+1)≥0.
化简并约去a2得(a2-1)m2-2bm+(1-b2)≥0.对任意m的值,要使这个式子永远成立,条件是
(1)
|
|
解得(1)
|
|
或(1)、(2)合写成:
|
故答案为
|
点评:此题主要考查直线及椭圆参数方程化简一般方程的问题,其中对于求公共点的问题可以把方程联立,然后根据判别式法求得取值范围,属于综合性试题,有一定的计算量.

练习册系列答案
相关题目
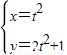 (t为参数)
(t为参数)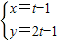 (t为参数)
(t为参数)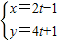 (t为参数)
(t为参数)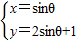 (θ为参数)
(θ为参数) (t是参数)椭圆(E)的参数方程是
(t是参数)椭圆(E)的参数方程是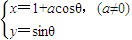 (θ是参数)问a、b应满足什么条件,使得对于任意m值来说,直线(L)与椭圆(E)总有公共点.
(θ是参数)问a、b应满足什么条件,使得对于任意m值来说,直线(L)与椭圆(E)总有公共点.