题目内容
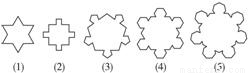
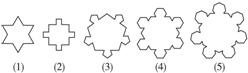
如图,第(1)个多边形是由正三角形“扩展”而来,第(2)个多边形是由正方形“扩展”而来…如此类推.设由正n边形“扩展”而来的多边形的边数为an,则a6=________;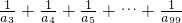 =________.
=________.
解:根据图形观察发现:
n边形“扩展”以后,每条边上又新增加了n条边,变成了n+n×n边形了,
即n边形“扩展”而来的多边形的边数
an=n+n2=n(n+1),所以a6=6×7=42.
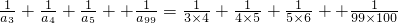
=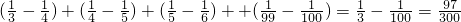 .
.
故答案为:42;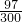 .
.
分析:通过观察前几个图形中新增加了边数得,n边形“扩展”以后,每条边上又新增加了n条边,变成了n+n×n边形了,从而求得an,及a6,再利用数列中拆项法结合求和公式即可解决求和问题.
点评:本题主要考查了归纳推理、数列的求和、数列递推式,以及分析问题解决的能力,属于基础题.
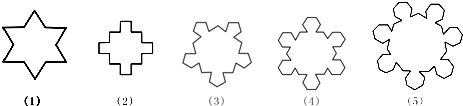
n边形“扩展”以后,每条边上又新增加了n条边,变成了n+n×n边形了,
即n边形“扩展”而来的多边形的边数
an=n+n2=n(n+1),所以a6=6×7=42.
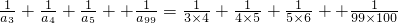
=
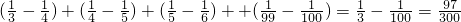 .
.故答案为:42;
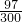 .
.分析:通过观察前几个图形中新增加了边数得,n边形“扩展”以后,每条边上又新增加了n条边,变成了n+n×n边形了,从而求得an,及a6,再利用数列中拆项法结合求和公式即可解决求和问题.
点评:本题主要考查了归纳推理、数列的求和、数列递推式,以及分析问题解决的能力,属于基础题.

练习册系列答案
相关题目
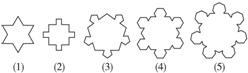
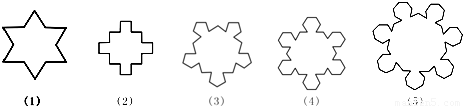
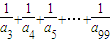 = .
= .