题目内容
过定点P（0，2），作直线l与曲线y2=4x有且仅有1个公共点，则这样的直线l共有 条．
【答案】分析：通过图象可知当直线与抛物线相切时，与x轴平行时和y轴时直线与抛物线有且仅有1个公共点．
解答：解：由题意可知过点p与x轴平行时直线与抛物线有一个交点；
当过点p与x轴不平行时设直线方程为y=kx+2，
与抛物线方程联立消去y得k2x2+（4k-4）x+4=0
要使直线与曲线有且仅有1个公共点需△=（4k-4）2-16k2=0，
解得k=
同时抛物线与y轴也只有一个交点，故y轴也符合；
故答案为3
点评：本题主要考查了抛物线的应用．本题可采用数形结合方法解决．
解答：解：由题意可知过点p与x轴平行时直线与抛物线有一个交点；
当过点p与x轴不平行时设直线方程为y=kx+2，
与抛物线方程联立消去y得k2x2+（4k-4）x+4=0
要使直线与曲线有且仅有1个公共点需△=（4k-4）2-16k2=0，
解得k=
同时抛物线与y轴也只有一个交点，故y轴也符合；
故答案为3
点评：本题主要考查了抛物线的应用．本题可采用数形结合方法解决．
练习册系列答案
相关题目
（a，b＞0）的左、右焦点分别为F1，F2，若P 是椭圆上的一点，
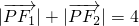，离心率
．
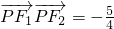，求点P的坐标；
（a，b＞0）的左、右焦点分别为F1，F2，若P 是椭圆上的一点，
，离心率
．
，求点P的坐标；