题目内容
用红、黄、蓝等6种颜色给如图所示的五连圆涂色,要求相邻两个圆所涂颜色不能相同,且红色至少要涂两个圆,则不同的涂色方案种数为( )
| A.610 | B.630 | C.950 | D.1280 |
B
解析试题分析:采用分类原理:第一类:涂两个红色圆,共有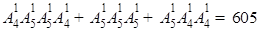 种;第二类:涂三个红色圆,共有
种;第二类:涂三个红色圆,共有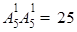 种;故共有630种.
种;故共有630种.
考点:排列、组合及简单计数问题.

练习册系列答案
相关题目
 6的展开式中x2的系数为( )
6的展开式中x2的系数为( )
| A.-240 | B.240 | C.-60 | D.60 |
从不同号码的三双靴中任取4只,其中恰好有一双的取法种数为 ( )
| A.12 | B.24 | C.36 | D.72 |
安排6名歌手演出顺序时,要求歌手乙、丙排在歌手甲的前面或者后面,则不同排法的种数是( )
| A.180 | B.240 | C.360 | D.480 |
现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张.从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张.不同取法的种数为( )
| A.232 |
| B.252 |
| C.472 |
| D.484 |
一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种数为( )
| A.3×3! |
B.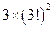 |
C.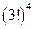 |
| D.9! |
若(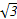 x-
x-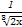 )n的展开式中含有非零常数项,则这样的正整数n的最小值是( )
)n的展开式中含有非零常数项,则这样的正整数n的最小值是( )
| A.3 | B.4 | C.10 | D.12 |
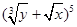 的二项展开式的第三项为
的二项展开式的第三项为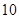 ,则
,则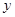 关于
关于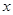 的函数图像大致形状为( )
的函数图像大致形状为( )