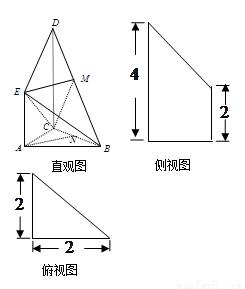题目内容
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视
图的侧视图、俯视图.在直观图中,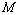 是
是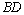 的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
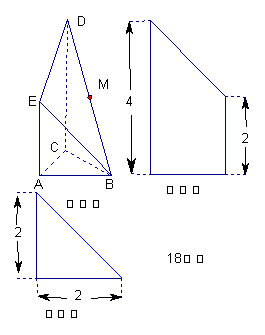 (1)求证:EM∥平面ABC;
(1)求证:EM∥平面ABC;
(2)试问在棱DC上是否存在点N,使NM⊥平面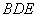 ?
若存在,确定点N的位置;若不存在,请说明理由.
?
若存在,确定点N的位置;若不存在,请说明理由.
(3)求二面角D—EB—A的大小的余弦值.
【答案】
解:由题意,Ea⊥平面ABC , DC⊥平面ABC ,AE∥DC,ae=2, dc=4 ,ab⊥ac,
且AB=AC=2 ……2分
|
(1)证明:∵m为db的中点,取bc中点G,连接em,mG,aG,
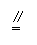 ∴ mG∥DC,且
∴ mG∥DC,且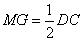
∴ mG ae,∴四边形aGme为平行四边形, 6分
∴em∥aG, 又AG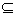 平面ABC ∴EM∥平面ABC.……4分
平面ABC ∴EM∥平面ABC.……4分
(2)由(2)知,em∥aG,
又∵平面BCD⊥底面ABC,aG⊥bc,∴AG⊥平面BCD
∴EM⊥平面BCD,又∵EM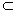 平面BDE,
平面BDE,
∴平面BDE⊥平面BCD
在平面BCD中,过M作MN⊥DB交DC于点N,
∴MN⊥平面BDE 点n即为所求的点 .……6分
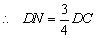 ∵
∵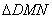 ∽
∽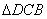
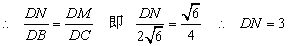
∴ 边DC上存在点N,满足DN=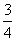 DC时,有NM⊥平面BDE. .…… 8分
DC时,有NM⊥平面BDE. .…… 8分
(3)2,3问均可以用向量办法解决,
第三问结果是 …… 12分
…… 12分

练习册系列答案
相关题目
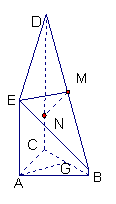
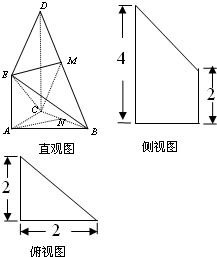 (2012•烟台三模)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(2012•烟台三模)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.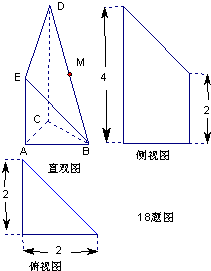 如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,M是BD的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,M是BD的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.

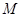 是
是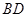 的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.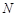 是
是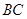 的中点,求证:
的中点,求证: 平面
平面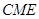 ;
;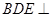 平面
平面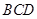 .
.