题目内容
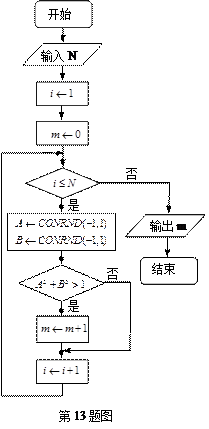
定义函数CONRND(a,b)是产生区间(a,b)内的任何一个实数的随机数函数.如图所示的程序框图可用来估计π的值.现在N输入的值为100,结果m的输出值为21,则由此可估计π的近似值为

3.16
3.16
.
分析:根据已知中CONRND(-1,1)是产生均匀随机数的函数,它能随机产生区间[-1,1]内的任何一个实数,及已知中的程序框图,我们可分析出程序的功能是利用随机模拟实验的方法求任取[-1,1]上的两个数A,B,求A2+B2>1的数对(A,B)的个数,分别计算出满足A∈[-1,1],B∈[-1,1]和A2+B2≤1对应的平面区域的面积,代入几何概型公式,即可得到答案.
解答:解:根据已知中的流程图我们可以得到
该程序的功能是利用随机模拟实验的方法求任取[-1,1]上的两个数A,B,求A2+B2>1的数对(A,B)的个数,
∵A∈[-1,1]B∈[-1,1]对应的平面区域面积为:2×2=4
而A2+B2≤1对应的平面区域的面积为:π
故
=
∴π≈
=3.16.
故答案为:3.16
该程序的功能是利用随机模拟实验的方法求任取[-1,1]上的两个数A,B,求A2+B2>1的数对(A,B)的个数,
∵A∈[-1,1]B∈[-1,1]对应的平面区域面积为:2×2=4
而A2+B2≤1对应的平面区域的面积为:π
故
| π |
| 4 |
| 100-21 |
| 100 |
| 79 |
| 25 |
故答案为:3.16
点评:本题考查的知识点是程序框图,其中根据已知中的程序流程图分析出程序的功能,并将问题转化为几何概型问题是解答本题的关键.

练习册系列答案
相关题目
 )是产生区间(
)是产生区间( 的值.现在N输入的值为1200,结果
的值.现在N输入的值为1200,结果 的输值为257,则由此可估计
的输值为257,则由此可估计


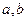 )是产生区间(
)是产生区间(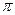 的值.现在N输入的值为1200,结果
的值.现在N输入的值为1200,结果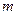 的输值为257,则由此可估计
的输值为257,则由此可估计