题目内容
某商场根据调查,估计家电商品从年初(1月)开始的x个月内累计的需求量p(x)(百件)为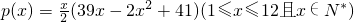
(1)求第x个月的需求量f(x)的表达式.
(2)若第x个月的消售量满足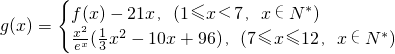 (单位:百件),每件利润
(单位:百件),每件利润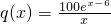 元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少?(e6取值为403)
元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少?(e6取值为403)
解:(1)x≥2时,f(x)=p(x)-p(x-1)=-3x2+42x;当x=1时,p(x)=39,也满足
∴f(x)=-3x2+42x,(1≤x≤12,x∈N*)
(2)设该商场第x个月的月利润为ω(x)元,则
1°当1≤x<7,x∈N*时,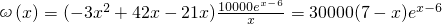 (5分)
(5分)
ω'(x)=30000(6-x)ex-6,令ω'(x)=0,∴x=6
∴ω(x)在[1,6]上单调递增,在[6,7]上单调递减
∴ω(x)max=ω(6)=30000(8分)
2°当7≤x≤12,x∈N*时,
ω'(x)=10000(x-12)(x-8)e-6,
∴ω(x)在[7,8]上单调递增,在[8,12]上单调递减
∴ω(x)max=ω(8)<30000(12分)
∴第6个月利润最大,是30000元 (13分)
分析:(1)利用f(x)=p(x)-p(x-1),可得第x个月的需求量f(x)的表达式.
(2)分类讨论,求得函数的最值,比较即可得到结论.
点评:本题考查函数模型的构建,考查导数知识的运用,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.
∴f(x)=-3x2+42x,(1≤x≤12,x∈N*)
(2)设该商场第x个月的月利润为ω(x)元,则
1°当1≤x<7,x∈N*时,
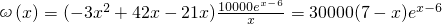 (5分)
(5分)ω'(x)=30000(6-x)ex-6,令ω'(x)=0,∴x=6
∴ω(x)在[1,6]上单调递增,在[6,7]上单调递减
∴ω(x)max=ω(6)=30000(8分)
2°当7≤x≤12,x∈N*时,

ω'(x)=10000(x-12)(x-8)e-6,
∴ω(x)在[7,8]上单调递增,在[8,12]上单调递减
∴ω(x)max=ω(8)<30000(12分)
∴第6个月利润最大,是30000元 (13分)
分析:(1)利用f(x)=p(x)-p(x-1),可得第x个月的需求量f(x)的表达式.
(2)分类讨论,求得函数的最值,比较即可得到结论.
点评:本题考查函数模型的构建,考查导数知识的运用,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
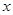 个月内累计的需求量
个月内累计的需求量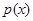 (百件)为
(百件)为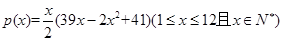
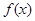 的表达式.
的表达式.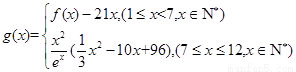 (单位:百件),每件利润
(单位:百件),每件利润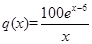 元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少?
元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少? 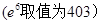

 (单位:百件),每件利润
(单位:百件),每件利润 元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少?(e6取值为403)
元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少?(e6取值为403)