题目内容
(1)设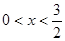 ,求函数
,求函数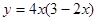 的最大值;
的最大值;
(2)已知x、y都是正实数,且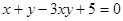 ,求
,求 的最小值.
的最小值.
(1)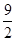 (2)
(2)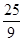
解析试题分析:(1)∵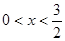 ,∴
,∴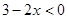 , ……1分
, ……1分
∴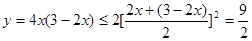 ,当且仅当
,当且仅当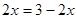 即
即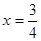 时,等号成立.
时,等号成立.
又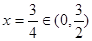 ……5分
……5分
∴函数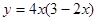 的最大值为
的最大值为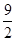 . ……6分
. ……6分
(2)由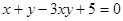 得
得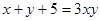 .
.
∵x、y都是正实数
∴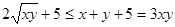 ,当且仅当
,当且仅当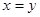 时,等号成立. ……8分
时,等号成立. ……8分
∴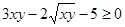
∴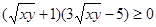
∴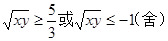
∴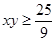 ,当且仅当
,当且仅当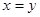 时,等号成立. ……10分
时,等号成立. ……10分
联立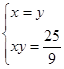 ,解得
,解得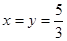 ……11分
……11分
∴当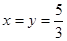 时,
时, 的最小值是
的最小值是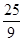 ……12分
……12分
考点:本小题主要考查基本不等式的应用.
点评:应用基本不等式求最值,要注意“一正二定三相等”三个条件缺一不可,另外还要注意一些特殊方法的应用,比如“1”的整体代换等.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 ,其中
,其中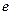 为自然对数的底数,
为自然对数的底数,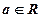 。
。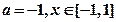 ,求函数
,求函数 的最值;
的最值; ,都有
,都有 成立,
成立, 的取值范围。
的取值范围。 ,
, ,
,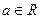
 时,求函数
时,求函数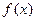 的最大值;
的最大值; ,且
,且 在
在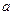 的取值范围.
的取值范围.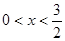 ,求函数
,求函数 的最大值;
的最大值;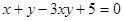 ,求
,求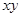 的最小值.
的最小值.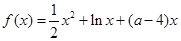 在
在 上是增函数.
上是增函数.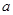 的取值范围;
的取值范围; ,求函数
,求函数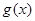 的最小值.
的最小值.