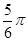题目内容
△ABC的内角A,B,C的对边分别为a,b,c,已知cos(A-C)+cosB=1,a=2c,则C=( )
A. 或
或 B.
B. C.
C. 或
或 D.
D.
B
解析

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
在△ 中, 若
中, 若 ,则△
,则△ 的形状是( )
的形状是( )
| A.直角三角形 | B.等腰三角形 | C.等腰直角三角形 | D.等边三角形 |
已知 中,
中, ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
在 中,
中, ,
, ,
, ,则边
,则边 的长为
的长为
A. | B. | C.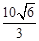 | D. |
在△ABC中,角A,B,C所对的边分别是a,b,c,若 ,则△ABC的形状是( )
,则△ABC的形状是( )
| A.等腰三角形 | B.直角三角形 | C.等腰直角三角形 | D.等腰或直角三角形 |
在 中,由已知条件解三角形,其中有两解的是( )
中,由已知条件解三角形,其中有两解的是( )
A.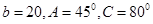 | B. |
C. | D. |
在 中,若
中,若 ,则
,则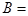 ( )
( )
A. | B. 或 或 | C. 或 或 | D. |
 中,角
中,角 的对边分别为
的对边分别为 ,若点
,若点 在直线
在直线 上,则角
上,则角 的值为( )
的值为( ) B.
B.