题目内容
一口袋内装有5个黄球,3个红球,现从袋中往外取球,每次取出一个,取出后记下球的颜色,然后放回,直到红球出现10次时停止,停止时取球的次数ξ是一个随机变量,则P(ξ=12)= .(填算式)
【答案】分析:若ξ=12,则取12次停止,第12次取出的是红球,前11次中有9次是红球,先考虑哪9次取红球,有C119种选择,又因为有10次取得是红球,乘以取红球的概率的10次方,还有2次取的是黄球,乘以取黄球的概率的平方.
解答:解:若ξ=12,则取12次停止,第12次取出的是红球,前11次中有9次是红球,
∴P(ξ=12)=C119( )9×(
)9×( )2×
)2× =
=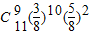
故答案为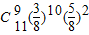
点评:本题考查了n次独立重复试验中某事件恰好发生k次的概率.
解答:解:若ξ=12,则取12次停止,第12次取出的是红球,前11次中有9次是红球,
∴P(ξ=12)=C119(
 )9×(
)9×( )2×
)2× =
=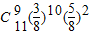
故答案为
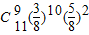
点评:本题考查了n次独立重复试验中某事件恰好发生k次的概率.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目